Här fortsätter vi titta på derivator.
Innehåll – Derivator:
1. Derivator
2. Sammansatta funktioner
3. Derivatan av en produkt
4. Derivatan av en kvot
1. Derivator
Nedan ser du de viktigaste deriveringsreglerna;
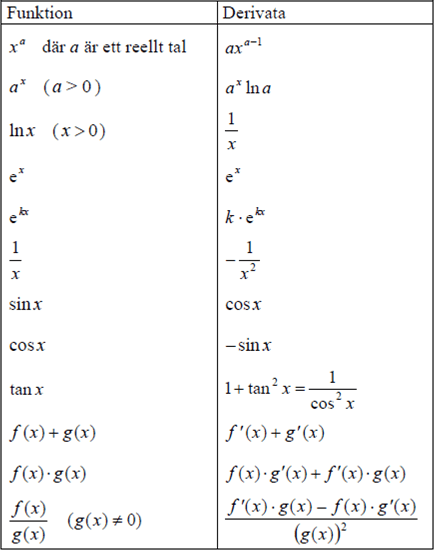
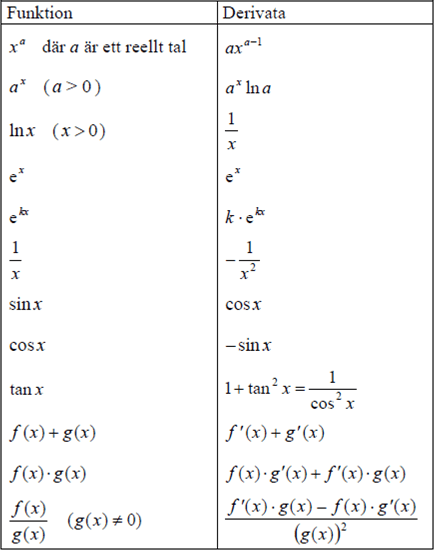
Andraderivatan
Andraderivatan är helt enkelt derivatan till en funktion som redan har blivit deriverad en gång. Andraderivatan skriver vi så här:
![]()
![]()
Det finns en rad andra beteckningar för andraderivatan förutom f’’(x).


Här nedan presenteras det första användningsområdet för andraderivatan:
Om en kropp rör sig utefter en rät linje och befinner sig s(t) meter från utgångsläget vid tiden t sekunder från starten gäller följande:
Kroppens hastighet är ![]()
![]()
Kroppens acceleration är ![]()
![]()
Exempel 1:
Beräkna ![]()
![]()
Vi får att: ![]()
![]()
Vi ska alltså räkna ut andraderivatan för y. D börjar vi med att räkna ut derivatan för y och deriverar sedan det nya uttrycket en gång till. Efter lite förkortningar så får vi fram det rätta svaret.
Exempel 2:
En hiss startar från bottenplanet och rör sig uppåt. Efter t sekunder har den flyttat sig s meter där ![]()
![]()
a) Hissen stannar när hastigheten är noll. Hur högt upp är hissen när den stannar?
b) Hur stor är hissens acceleration när den startar?
Lösning:
a) För att få fram hur långt upp hissen har åkt måste vi ju veta hur länge den har åkt. Det är alltså tiden t sekunder som vi först måste få reda på. Den enda info vi har fått är att hastigheten är noll då hissen stannar. Vi behöver därmed en formel för hissens hastighet för att ha något att räkna på. Om vi kikar på reglerna i början på stycket så ser vi att vi kan få fram ett uttryck för hastigheten genom att derivera uttrycket för sträckan, och uttrycket för sträckan är just det vi har. Då vi har fått fram formeln för hastigheten så sätter vi den lika med noll och kan då räkna ut tiden t.
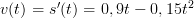
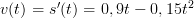
Vi sätter derivatan lika med noll ![]()
![]()
Efter faktoriseringen ser vi tydligt att ![]()
![]()


Vi faktoriserar, alltså bryter ut t och sätter det framför parentesen, nu är antingen t=0 eller parentesen=0. Som väntat får vi två olika svar eftersom hastigheten är noll dels innan den startar (t=0), dels då den stannar (t=6). Den stannar alltså efter 6 sekunder. För att ta reda på hur långt hissen hinner färdas på 6 sekunder sätter vi helt enkelt t=6 i vårt uttryck för sträckan:
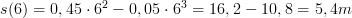
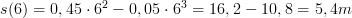
Svar: Hissen stannar 5,4 meter upp i luften.
b) enligt reglerna ovan så är accelerationen lika med derivatan av uttrycket för hastigheten. (Man kan även säga att accelerationen är andraderivatan av uttrycket för sträckan eftersom vi deriverar uttrycket för sträckan för att få fram uttrycket för hastigheten och sedan deriveras detta uttryck i sin tur för att få fram accelerationen). Uttrycket för hastigheten räknade vi ut i a-uppgiften så vi tar bara och deriverar detta.


Då hissen startar har det ännu inte hunnit gå någon tid vilket gör att vi kan sätta att t=0 och sedan föra in det i uttrycket a(t) och räkna ut accelerationen:




Svar: Hissens acceleration är 0,9 m/s2.
2. Sammansatta funktioner
Då en funktion är lite mer komplicerad så kan vi som tur var dela upp den i två eller flera funktioner och därmed blir den lättare att lösa.
Exempel 1:
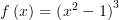
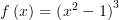
Beräkna f(2)
Se parentesen med x2-1 som en funktion, z, 

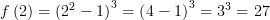
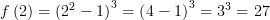
Svar: 

Derivatan av sammansatta funktioner
Då man deriverar sammansatta funktioner så kan man antingen derivera funktionen efter att man har utvecklat den eller så deriverar man direkt. Då man deriverar den direkt måste man dock ofta ta hänsyn till den yttre och den inre derivatan.
Exempel 2:
Beräkna derivatan av 

Vi börjar med den yttre derivatan och flyttar alltså ner tvåan framför parentesen. Innehållet i parentesen skriver vi som förut. Den inre derivatan är alltså derivatan av det inuti parentesen. I detta fallet får vi kvar 5 efter att ha deriverat innehållet i vår parentes. Den inre derivatan skrivs alltid efter parentesen och den skrivs som att man multiplicerar den med resten. Den multipliceras alltså med tvåan och parentesen.
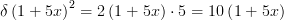
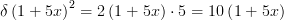
Derivatan är alltså 

3. Derivatan av en produkt
Då vi deriverar en produkt av två olika funktioner så måste vi använda oss utav följande regel.
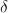
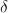


u(x) och v(x) symboliserar två olika funktioner.
Notera att det ska vara två funktioner! Står det 4 · f(x) så är det inte två funktioner man multiplicerar eftersom 4 bara är en konstant.
Exempel 1:
Bestäm derivatan
a) 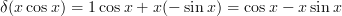
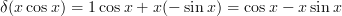
b) 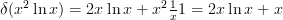
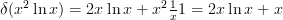
Glöm inte bort den inre derivatan i ln x i uppgift b
4. Derivatan av en kvot
Då vi deriverar en kvot av två olika funktioner så måste vi använda oss utav följande regel.


u(x) och v(x) symboliserar två olika funktioner.
Notera även här att det ska vara två funktioner! Står det f(x)/4 så är det inte två funktioner man dividerar eftersom 4 bara är en konstant.
Exempel 1:
Beräkna derivatan av
a)

a)

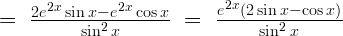
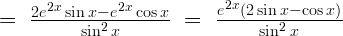
I slutet på b-uppgiften faktoriserar vi, alltså vi bryter ut faktorn e2x eftersom den fanns i båda talen. Det finns även ett specialfall här. Då täljaren är konstant lika med 1 så gäller detta:


Exempel 2:
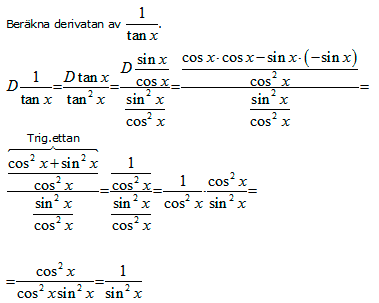
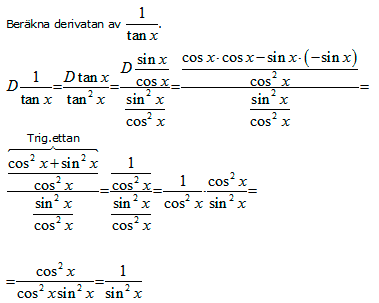
Det första vi gör är att ta hänsyn till undantagsregeln som jag visade här ovan. Den gör så att vi får Derivatan av (tan x) i täljaren. Sedan skriver vi om tanx till sinx/cosx enligt en formel vi tidigare har lärt oss. Vi låter nämnaren vara för ett tag för att koncentrera oss på uträkningen av derivatan av sinx/cosx. Då vi räknar ut den derivatan måste vi tänka på regeln för derivatan av en kvot. Efter deriveringen så ser vi att i övre täljaren får vi ett uttryck som ser ut som trig.ettan vilket gör att det blir lika med 1. I nästa steg kan vi jämföra det vi ser med att dividera bråktal. Vi multiplicerar därmed täljare med nämnare, och vi får inte glömma att invertera, alltså vända på nämnaren. Efter detta så kan vi lätt förkorta bort cos2x och få kvar 1/sin2x .
Nedan visar jag samma uträkning fast jag hoppar över steget där vi räknar ut derivatan av tangens eftersom man lika gärna kan slå upp den i formelsamlingen.
Exempel 3:
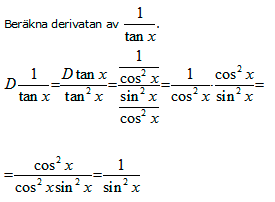
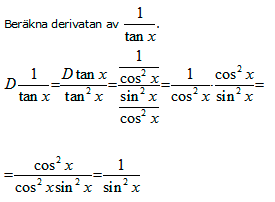
OBS!
Att derivatan av tan x = 1/cos2x kan vara bra att lägga på minnet. Den finns även att slå upp i formelsamlingen.

