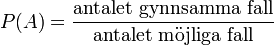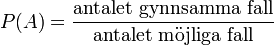Sannolikhetslära och statistik är två relativt nya begrepp som introduceras i matematik 2. Slumpförsök påvisar bland annat tveksamheten i att spela på roulette medan vi också går in på statistiska begrepp som median och medelvärde. Ha så skoj!
Innehåll – Sannolikhetslära och statistik:
1. Statistik
2. Slumpförsök
1. Statistik
Statistik är “Läran om siffror och dess förhållande till verkligheten”.
Det tas upp några olika mätvärden så som:
Median: De tal som av värde är i mitten, vid två tas medelvärdet ut av dem.
Medelvärde: Summan av talen dividerat på antal värden.
Typvärde: De tal som förekommer mest.
Om du inte känner till dessa mätvärden, rekommenderar vi dig att ta en titt på matematik A under fliken ”median och medelvärde”.
Bias och Bortfall är exempel på olika faktorer som kan påverka resultatet/slutsatsen utav en statistik undersökning. Bias är systematiska fel i insamlandet och tolkningen av data och bortfall kan påverka resultatet genom att viktig information inte tas upp.
2.Slumpförsök


Sannolikhet betecknar, i matematisk mening, väntevärdet för en stokastisk händelse.
Ett vanligt exempel på sannolikhet är singlandet av ett mynt, där det förmodas att myntet ska hamna med krona upp på hälften av alla kast, och klave upp på andra hälften. Detta kan baseras på att myntet antas vara symmetriskt, så att det är lika troligt att det ska visa krona som klave, eller att man, baserat på tidigare kast, drar slutsatsen att, eftersom de hittills utförda kasten givit ett utfall där antalet visade kronor är lika stort som antalet klavar, alla framtida kast kommer att fortsätta i samma mönster. Det tidigare kallas en ”subjektivt angiven sannolikhet”, då den baseras på ett antagande om symmetri, till skillnad från det senare, som är en ”objektivt angiven sannolikhet”, baserat på empiri och utförda experiment.
Bestämning av sannolikheter
Alla beräkningar med sannolikhet baseras på Kolmogorovs axiom, varifrån man kan härleda två principiellt olika sätt att bestämma en sannolikhet för att händelse A ska inträffa:
Sannolikhetsfunktionen lyder som nedan där P(A) står för sannolikheten att utfall A inträffar.