Funktioner är ett välkänt ämne för er som läst Matematik 1 men här kommer lite nyheter inom området som gör er ännu skarpare! Ha skoj!
Innehåll – Funktioner:
1. Linjära funktioner
2. Linjära ekvationssystem
3. Andragradsfunktioner
1. Linjära funktioner
Med ordet funktion inom matematiken menas en regel där man stoppar in ett värde för att få ut ett annat. Till exempel så är polynomet som vi hade tidigare,
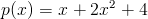
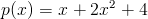
en funktion. Här kan vi stoppa in värdet 3 för att sedan få ut ett nytt värde:
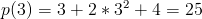
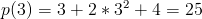
Varje värde på x ger exakt ett p-värde, man säger att p är en funktion av x.
Om vi tänker oss en taxiresa som kostar 30 kr i startavgift och 25 kr för varje kilometer som är körd så kan vi om vi kallar sträckan för x och slutpriset för y ställa upp följande samband:


Om vi ritar upp grafen för taxiresan så ser den ut så här:
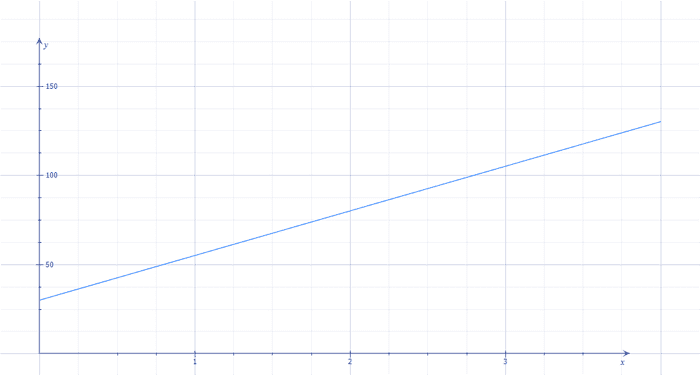

Vi ser att priset som vi har på y-axeln ökar linjärt med sträckan som vi har på x-axeln. Detta kallas för en linjär funktion och alla dessa kan skrivas på ett gemensamt sätt:
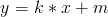
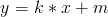
Detta kallas för räta linjens ekvation. K är den koefficient som skrivs före x och det motsvarar i grafen lutningen på linjen och brukar kallas för riktningskoefficient. M är en konstant som i grafen motsvarar den räta linjens skärning med y-axeln.
I vårt exempel så är k = 25 och m = 30.
Hur löser vi då frågan: hur mycket kostar en 3 kilometer lång taxiresa?
Det finns två lösningar på frågan, en grafisk och en algebraisk.
Den grafiska lösningen är att vi letar upp x = 3 i grafen och läser av vad y blir i samma punkt, y = 105 kr.
Den algebraiska lösningen innebär att vi helt enkelt sätter in 3 i vår ekvation:
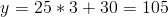
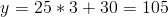
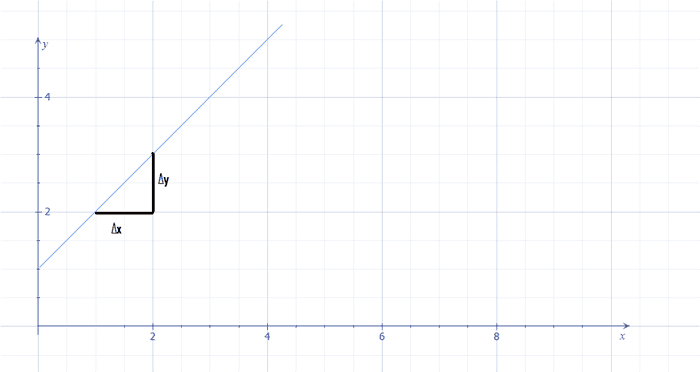
Hur gör man då för att beräkna riktningskoefficienten? Jo riktningskoefficienten, k, beräknar vi genom att dividera förändringen i y-led, Δy med förändringen i x-led, Δx:



En annan formel för k som man kan använda när man bara känner till två punkter på linjen är:
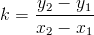
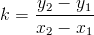
Nu ett exempel som beskriver hur man räknar ut k:
Beräkna k för följande punkterna, (2,2) och (4,4). Om vi plottar dessa och drar en linje där i mellan får vi följande graf:
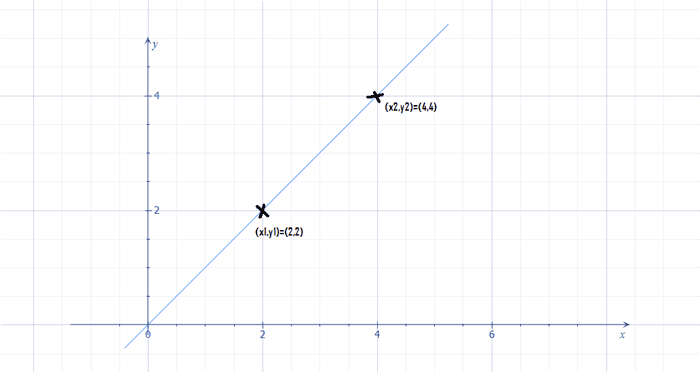

Vi sätter in våra värden på punkterna i ekvationen för k:
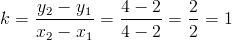
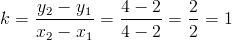
Värdet på m kan vi avläsa i grafen dvs den punkt där linjen skär y-axeln, vi ser enkelt att m = 0. (Om man inte har ritat upp grafen kan man sätta in en känd punkt (x,y) och k-värdet i formeln: y = k · x + m och på så sätt räkna ut m)
Vi får då ekvationen:
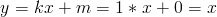
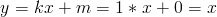
2. Linjära ekvationssystem
Här nedan ser vi ett så kallat ekvationssystem. Det är två ekvationer och ”klammern” är till för att visa att y har samma värde.


Vi kan lösa ekvationssystemen på två sätt; algebraiskt eller grafiskt. Båda sätten är relativt enkla.
Grafisk lösning
En grafisk lösning av ekvationssystem bygger helt enkelt på att man bestämmer skärningspunkten mellan linjerna med de två ekvationerna. Det är koordinaterna i skärningspunkten som utgör lösningen till ekvationssystemet.
Exempel 1:
Lös ekvationssystemet 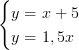
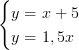
Lösning:
Rita upp de båda linjerna antingen på ett papper eller i miniräknaren.
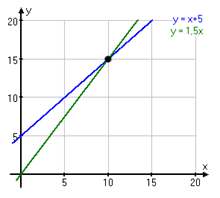

Linjerna har ekvationerna ![]()
![]()
![]()
![]()
Skärningspunkten mellan linjerna har koordinaterna x = 10 och y = 15, vilket innebär att lösningen till systemet är x = 10 och y = 15.
Svar: x = 10 och y = 15.
Algebraisk lösning
Detta sätt att lösa ekvationssystem kan ibland vara att föredra eftersom det ger ett exakt värde på lösningen och kan även vara enklare att genomföra.
Exempel 2:
Lös ekvationssystemet 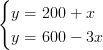
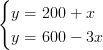
Lösning:
Sätt båda y-värdena lika med varandra.


För att få fram y så sätter vi in bara in x-värdet i en utav ekvationerna.
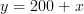
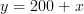
Insättning ger:
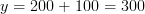
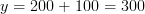
Svar: 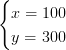
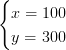
Algebraisk lösning – Additionsmetoden
Additionsmetoden bygger på att vi adderar de båda vänsterleden och sätter dem lika med de båda adderade högerleden.
Exempel 3:
Lös ekvationssystemet 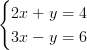
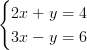
Lösning:
Då vi adderar de båda ekvationerna ser vi att y-termerna försvinner och vi kan då lösa ut x.
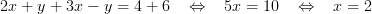
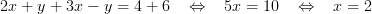
För att sedan få fram y-värdet så sätter vi in x-värdet i en utav ekvationerna:
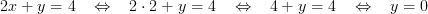
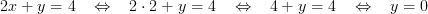
Svar: 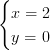
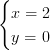
Ibland måste man dock multiplicera ekvationerna med lämpliga tal för att additionsmetoden ska fungera.
Exempel 4:
Lös ekvationssystemet 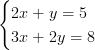
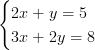
Lösning:
Här multiplicerar vi den första ekvationen med 3 och den andra med -2. Det gör vi för att koefficienterna hos x-termerna blir motsatta tal och därmed försvinner x-termerna. Vi skulle även kunna använda samma metod för att utesluta y.
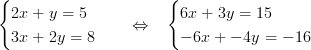
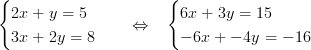
Nu tillämpar vi additionsmetoden och får följande resultat:


Sätt in y = 1 i en av ekvationerna:
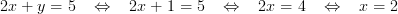
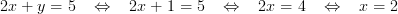
Svar: 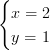
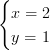
Algebraisk lösning – Substitutionsmetoden
Denna metod bygger på att vi löser ut antingen x eller y i den första ekvationen och ersätter den termen i den andra ekvationen med det uttryck man får.
Exempel 5:
Lös ekvationssystemet 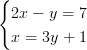
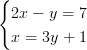
Lösning:
Vi löser ut y i den första ekvationen…
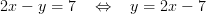
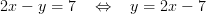
…och ersätter y i den andra ekvationen med det uttryck vi fick fram:


Nu när vi vet vad x har för värde så kan vi också beräkna värdet på y:
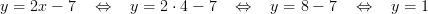
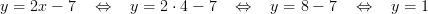
Svar: 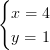
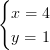
3. Andragradsfunktioner
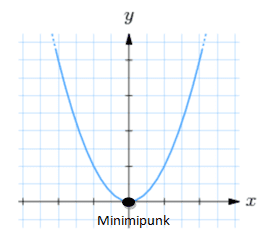

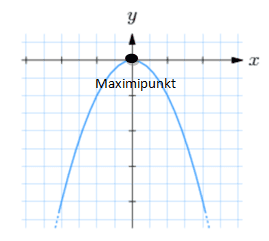

Här ser du två andragradsfunktioner. Man kallar det minsta värdet för minimipunkten och det största för maximipunkten.

