Inledning
I det förra kapitlet tittade vi laddningar, vilka är grunden för att elektricitet ska kunna uppkomma, så det är ju bra! Elektrisk ström, som hela vårt samhälle bygger på idag, är egentligen något så simpelt som laddningar som rör på sig. I detta kapitel för Fysik 1 ska vi titta lite mer på hur laddningar kan röra sig och hur ström uppkommer och utnyttjas i olika sammanhang.
Ström
Definitionen av ström är hur stor laddning som passerar en viss punkt av ledningen på en viss tid. Ju större laddning som passerar inom tidsintervallet, desto större är strömmen.
Enheten blir 
vilket motsvarar 1 Ampere(
).
Små och stora strömmar
Det är lätt att luras att tro att en ström är ofarlig bara för att laddningsmängden är liten. Ta en blixt till exempel; laddningen är inte så stor vid ett blixtnedslag på grund av att blixtnedslaget varar så kort tid. Den korta tiden gör dock att strömmen ändå blir väldigt stor och därför är blixtnedslaget livsfarligt!
Strömriktning
I förra kapitlet pratade vi om att det är ledningselektronerna som kan röra sig och ge en ström. När man ritar en strömkrets borde man ju därför sätta strömriktningen som elektronerna rör sig, dvs. från minus till plus, men det gör man inte! Man gör precis tvärtom då detta bestämdes långt innan man visste att det fanns elektroner.
Strömriktningen i ett kopplingsschema ska alltid ritas såsom en positiv laddning skulle rört sig, dvs. från plus till minus.
Spänningskälla
Nu tänker vi oss att vi kopplar en krets med enbart ett batteri likt bilden ovan. Elektroner kommer då glatt att röra sig från minuspol till pluspol(fast man ritar strömriktningen motsatt). Men till slut borde ju alla elektroner ha vandrat till pluspolen, och då kan ju ingen ström gå mer, eller? Nej, så fungerar det som tur är inte! Batteriet har kemisk energi i sig som kan användas till att transportera elektroner från pluspolen till minuspolen, så att elektronerna kan flyta genom kretsen igen. Detta fortgår tills den kemiska energin i batteriet är slut på kemisk energi.
Nu kommer en liknelse som vi själva har kommit på, så ni får ta den med en nypa salt:
Man kan tänka sig en slalombacke där människorna som åker nerför backen är laddningar. Batteriet(spänningskällan) är liften som transporterar de glada skidåkarna upp igen.
Energi och effekt
Energi
”Allt kostar pengar” fick jag lära mig redan i unga år, men det är inte riktigt sant för att driva elektriska kretsar kostar energi! När till exempel en lampa lyser kommer den elektriska energin som passerar den i form av elektronerna att värma upp glödtråden så att den lyser. Elektrisk energi omvandlas alltså till värmeenergi.
Nu ska vi titta på hur man kan ta reda på hur mycket energi som förbrukas när lampan lyser:
I föregående kapitel lärde vi oss att:
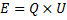
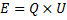
I det här kapitlet lärde vi oss:
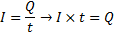
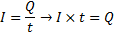
Vi ersätter 
med 
och får:
Effekt
Vi ska traska vidare och härleda en formel för effekten som utvecklas i kretsen.
Nyss konstaterade vi att:
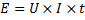
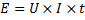
I förra kapitlet fastslog vi att:
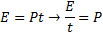
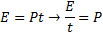
Vi ersätter 
med 
och får:
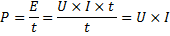
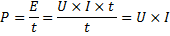
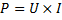
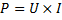
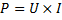
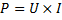
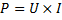
Likström och växelström
Hittills har vi beskrivit likström, där vi i kopplingsschemat har strömriktningen som en positiv laddning skulle rört sig, dvs. från pluspol till minuspol. I batteriet dras sedan laddningarna från minuspol till pluspol.
I vardagen används dock oftare växelström som går ut på att pluspol och minuspol regelbundet byter plats. Detta gör att laddningarna rör sig korta sträckor fram och tillbaka. Vi kallar den takt som polerna byter plats i för frekvens(svängningar per sekund). Enheten kallas för hertz(Hz). I vanliga vägguttag har vi växelström och där är frekvensen 50 Hz, vilket innebär att strömriktningen ändras 100 gånger per sekund.
Du kan använda formlerna för effekt och energiomsättning även för växelström, men du får du effektivvärden, som vi kommer gå mer fördjupat in på i Fysik 2.
Att mäta ström och spänning
Ström
För att mäta strömmen i en krets använder man en amperemeter. Denna ska seriekopplas med kretsen på grund av att all ström som går genom kretsen även ska gå genom amperemetern.
BILD på sidan 232, markerad som c.
Spänning
Spänningen mäts med en voltmeter. Denna ska kopplas parallellt med den det av kretsen man vill mäta spänningen över. I bilden nedan har vi parallellkopplat voltmetern med lampan, vilket gör att vi mäter spänningen över lampan.
Ohm’s lag
Nu ska vi titta på ett känt samband mellan strömmen och spänningen i en krets, nämligen Ohm´s lag. För att göra detta ska vi ordna ett litet experiment.
Vi kopplar ihop en spänningskälla där spänningen kan varieras med en amperemeter och en voltmeter. Vi börjar med en låg spänning och noterar på amperemetern hur stor strömmen blir. Sedan ökar vi successivt och noterar motsvarande ökning i ström.
Om vi ritar in punkterna i en graf får vi följande utseende:
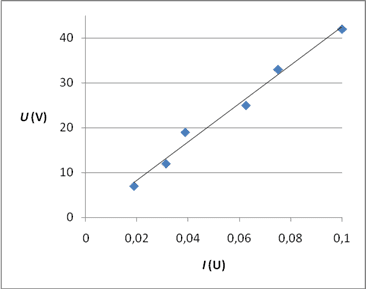
Vi ser att sambandet är linjärt och går genom origo(koordinaten 0,0). Nu undrar ni förstås vad konstanten är som ger grafen sin lutning. Det är faktiskt resistansen(R), eller med andra ord motståndet i kretsen. Resistansen är det motstånd laddningarna har när de flyter genom kretsen.
Ohm´s lag:
Enheten för resistans är 1 ohm(
)
Exempel
I bilden nedan har vi ett kopplingsschema. Beräkna utifrån givna värden den utvecklade effekten i kretsen.
Lösning
Först räknar vi ut strömmen som går i kretsen:
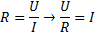
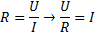
Sedan tidigare vet vi att:
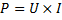
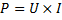
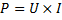
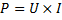
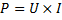
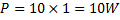
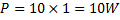
Svar: Effekten som utvecklas i kretsen är 10 watt.
Följ länken för att nå en video som på ett enkelt och bra sätt beskriver Ohm´s lag.
Elektrisk effekt i resistorer
Nu ska vi leka lite med de formler vi har lärt oss! En resistor är en komponent som ger resistans i en krets. Nu ska vi titta på två alternativa sätt att räkna på effekten som förbrukas i en resistor.
Den klassiska varianten är ju:
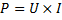
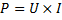
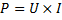
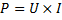
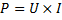
Men nu vet ju vi att man, enligt Ohm´s lag, lika väl kan skriva om spänningen och strömmen på följande vis:
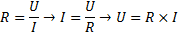
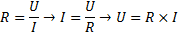
Om vi börjar med att ersätta 
med 
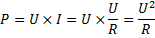
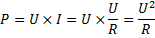
Nu ersätter vi istället 
med 
och ser vad som händer!
Nu har vi hittat två nya sätt att räkna på effekten i resistorer:
Exempel
Elektrikern Jacob kopplar en resistans på 
som tål 
till en krets. Hur stor spänning tål resistorn?
Lösning
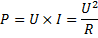
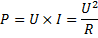
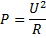
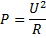
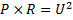
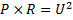
Svar: Ungefär 280 V. Tänk på att du alltid måste avrunda neråt när det gäller dessa typer av uppgifter då du inte får svara med ett större svar än kretsen tål.
Resistans i metalltråd
Det kan vara mycket vettigt att kunna räkna på resistansen i en metalltråd då denna ofta fungerar som ledare. Vi ska försöka resonera oss fram till vilka faktorer som bör påverka resistansen. Här kommer några tankar:
1. Trådens längd bör ju påverka. En längre tråd bör göra att laddningarna hinner kollidera fler gånger och tappa hastigheten. Alltså borde resistansen öka med trådlängden.
2. En tjockare tråd borde göra att fler laddningar kan passera den samtidigt. Alltså borde resistansen minska om tråden är tjockare.
3. Olika metaller leder ju ström olika bra. Därför borde metallsorten även spela roll för hur stor resistansen är.
Faktum är att det är dessa tre faktorer som avgör resistansen i metalltråden:
(lilla rå) är i denna formel metallens resistivitet, vilket är ett mått på metallens förmåga att leda ström. En låg resistivitet innebär att metallen leder ström bra. En hög resistivitet innebär en dålig ledare.
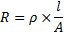
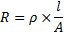
Så var det med den saken!
Serie- och parallellkopplingar
Nu kommer vi kanske till kapitlets höjdpunkt, serie- och parallellkopplingar, så lystra! Vi ska titta på hur man bygger serie- och parallellkopplingar samt hur man räknar på olika saker.
Seriekopplingar
En seriekoppling är när man kopplar elektriska komponenter i serie, det vill säga efter varandra. Vi tittar på kopplingsschemat nedan, där vi seriekopplat tre stycken lampor med spänningskällan.
Strömmen
Om vi först tittar på hur stor strömmen blir i olika delar av kretsen kan vi direkt konstatera att eftersom inga laddningar försvinner så kommer samma antal laddningar att gå genom resistor 1 som 2 och 3. Strömmen måste alltså vara lika stor överallt i den seriekopplade kretsen. Laddningarna har ju bara en väg att gå och alla kommer därför passera alla punkter av kretsen.
Alltså: Strömmen är lika stor överallt i den seriekopplade kretsen.
Spänningen
Spänningen är olidlig att få veta hur stor spänningen är i en seriekopplad krets! När vi pratar om spänningar måste vi prata om delspänningar. Över varje resistor kommer det att ligga en delspänning, och alla delspänningar tillsammans ger den totala spänningen i kretsen som ligger över spänningskällan.
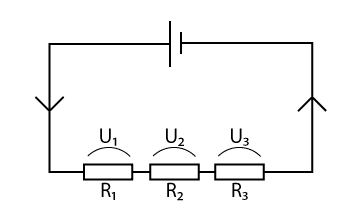
Resistansen
Alla tre resistorer i vårt kopplingsschema kommer att bidra till en totalresistans i kretsen. Totalresistansen brukar kallas för ersättningsresistansen.
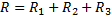
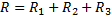
Exempel
Tre resistorer är seriekopplade enligt kopplingsschemat nedan. Beräkna utvecklade effekten i kretsen.
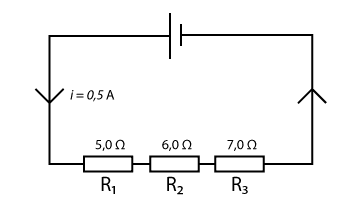
Lösning
Först måste vi lura ut hur stor spänningen är i kretsen. Detta gör vi genom Ohm´s lag som säger att:
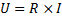
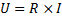
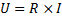
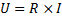
Eftersom det är en seriekoppling är strömmen lika stor överallt i kretsen och:
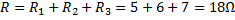
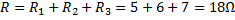
Om strömmen är 
så gäller:
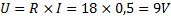
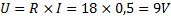
Sedan vet vi sedan tidigare att:
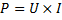
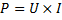
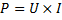
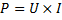
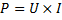
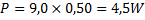
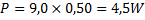
Svar: Effekten är 4,5 watt.
Parallellkoppling
I en parallellkoppling kopplas elektriska komponenter parallellt med varandra. Man delar upp vägen för laddningarna i två eller flera delar liksom. Vi ska även här titta på hur stor ström, spänning och resistans blir.
Strömmen
Nu kommer ju laddningarna att ha flera vägar att välja på. I vår bild kommer laddningarna att fördela sig på väg ett, två och tre, vilket ger upphov till I1, I2 och I3. Eftersom inga laddningar försvinner kommer all ström att gå genom de olika vägarna:
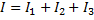
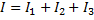
Spänningen
Vi tänker bara konstatera att spänningen är lika stor över alla resistorer som är med i parallellkopplingen.
Resistansen
Nu tänker vi oss att resistorerna har resistanserna R1, R2 och R3.
Om vi använder ersättningsresistansen för parallellkopplingen så vet vi enligt Ohm´s lag att:
Eftersom vi vet att spänningen är lika stor över alla resistorer som är parallellkopplade an vi då glatt konstatera att:
kan skrivas som:
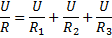
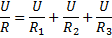
Vi kan dividera bägge led med och få att:
Exempel
Uppgift 9.31 i fysikboken Heureka! är alldeles utmärkt!
Två resistorer är parallellkopplade enligt figuren. Strömmen genom den större resistansen är 
.
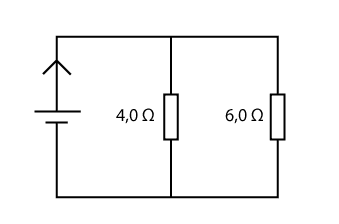
a) Hur stor är spänningen över resistorerna?
b) Hur stor är strömmen genom den mindre resistorn?
c) Hur stor är strömmen genom spänningskällan?
Lösning
a) Hur stor är spänningen över resistorerna?
De bägge resistorerna är parallellkopplade med spänningskällan.
Spänningen över den större resistorn är enligt Ohm´s lag:
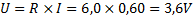
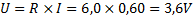
Eftersom spänningen är lika stor över alla komponenter som är parallellkopplade är spänningen 3,6 volt även över andra resistorn samt över spänningskällan.
Svar: Spänningen är 3,6 volt.
Hur stor är strömmen genom den mindre resistorn?
Eftersom vi vet att spänningen över den mindre resistorn (liksom över den större) är 3,6 volt och att resistansen i den mindre resistorn är 4,0 ohm så kan vi återigen använda Ohm´s lag:
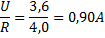
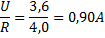
Svar: Strömmen genom den lilla resistorn är 0,90 ampere.
c) Hur stor är strömmen genom spänningskällan?
I en parallellkoppling kommer:
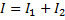
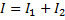
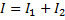
Detta gäller som tidigare sagt för att ledningselektronerna bara kan ta dessa två vägar, och inga elektroner försvinner.
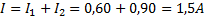
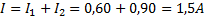
Svar: Den totala strömmen genom spänningskällan är 1,5 ampere
Lite kuriosa
Om en lampa går sönder som är seriekopplad kommer strömmen brytas i alla seriekopplade lampor på grund av att strömmen inte kan ta någon annan väg än genom den glödtråd som har brustit. Om lamporna istället är parallellkopplade kommer bara en av vägarna att försvinna när lampan går sönder. Då kommer de andra lamporna att lysa starkare då fler elektroner går genom dem, och alltså en större ström.
Att kombinera kunskaper
Ibland kan det vara utmärkt att kunna kombinera sina kunskaper, och i exemplet nedan ska du få chansen att kombinera dina kunskaper i serie- och parallellkopplingar!
Tips: När du gör nedanstående uppgifter kan det vara smart att använda de två rutorna som sammanfattar spänning, ström och resistans för seriekopplade, respektive parallellkopplade resistorer.
Exempel 1
Detta exempel är också taget från den utmärkta fysikboken Heureka! Uppgiften är i boken 9.32 och lyder som följer:
Tre resistorer har resistanserna 18 ohm, 20 ohm och 30 ohm. De har kopplats enligt figuren och ansluts till spänningen 15V.
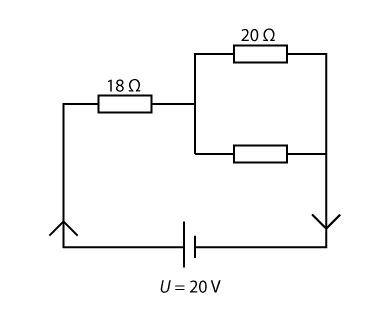
a) Beräkna ersättningsresistansen.
b) Hur stor är strömmen genom resistorn med resistansen 18 ohm?
c) Beräkna strömmen genom var och en av de parallellkopplade resistorerna.
Lösning
a) Beräkna ersättningsresistansen.
Vi börjar med att beräkna ersättningsresistansen för de bägge parallellkopplade resistorerna. För dessa gäller:
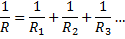
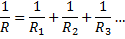
För oss ger detta:
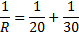
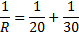
Genom förlängning till minsta gemensamma nämnare får vi:
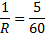
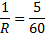
Om vi inverterar dessa får vi:
Denna resistans är enligt figuren seriekopplad med en resistor på 18 ohm.
För seriekopplade resistorer gäller:
I vårt fall ger detta:
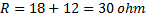
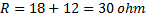
Svar: Totalresistansen(ersättningsresistansen) i kretsen är 30 ohm.
b) Hur stor är strömmen genom resistorn med resistansen 18 ohm?
Lösning
Eftersom denna resistor är seriekopplad med spänningskällan kommer alla ledningselektroner att gå genom den. All ström i kretsen kommer alltså att gå genom den.
Vi vet att spänningen över spänningskällan är 15V och att totalresistansen i kretsen är 30 ohm.
Ohm´s lag säger:
Detta ger för oss:
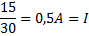
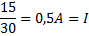
Svar: Strömmen genom resistorn är totalströmmen i kretsen, nämligen 0,5A.
c) Beräkna strömmen genom var och en av de parallellkopplade resistorerna.
Av de 0,5 ampere som går genom kretsen kommer en del att välja att gå genom vardera av de två parallellkopplade resistorerna. För att räkna på hur stor ström som går genom de bägge resistorerna måste vi först veta hur stor spänning som ligger över dem(spänningen blir lika stor över bägge då de är parallellkopplade):
De parallellkopplade resistorerna är seriekopplade med resistorn på 18 ohm. Vi kan lätt räkna ut spänningen över denna:
(vi vet sedan tidigare att strömmen genom resistorn är 0,5A, se b)).
I en seriekoppling gäller att:
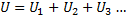
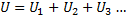
Vi vet att totalspänningen över batteriet är 15 V. I vårt fall:
Spänningen över de bägge parallellkopplade resistorerna är således 6V.
Nu är kan vi enkelt räkna ut strömmen genom de bägge resistorerna då vi vet resistanserna och spänningen:
För den på 20 ohm gäller:
Detta ger:
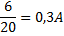
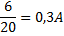
För den på 30 ohm gäller:
Detta ger:
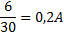
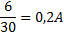
Svar: Strömmarna genom de bägge resistorerna är 0,3A genom den mindre av de parallellkopplade resistorerna och 0,2A genom den större av de två.
Exempel 2 (lite jobbigare!)
Beräkna spänningarna över resistorerna i figuren nedan:
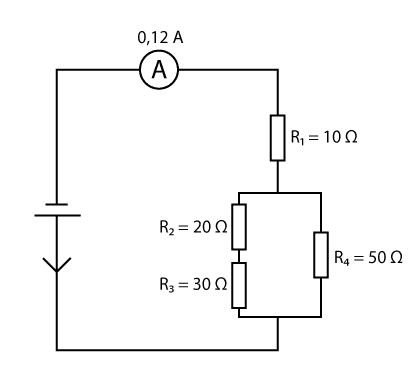
Lösning
Spänningen över R1:
Denna resistor är seriekopplad med spänningskällan vilket innebär att all ström går genom den. Enligt Ohm´s lag är:
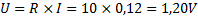
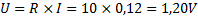
Nu måste vi räkna ut ersättningsresistansen för den parallellkopplade delen där R2, R3 och R4 ingår:
R2 och R3 är dock seriekopplade i parallellkopplingen och deras totala resistans är:
R4 har också resistansen 50 ohm.
Vi kan alltså säga att vi har två parallellkopplade resistorer på vardera 50 ohm.
Parallellkopplade resistorer har ersättningsresistansen:
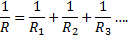
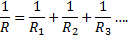
För oss ger detta:
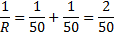
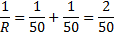
Genom att invertera (vända på) detta får vi att:
Ersättningsresistansen i den parallellkopplade delen är alltså 25 ohm.
Denna ersättningsresistans är seriekopplad med R1på 10 ohm och den totala resistansen i kretsen är således:
….
För oss ger detta att
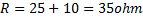
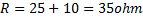
Den totala spänningen i kretsen blir då enligt Ohm´s lag:
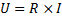
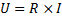
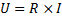
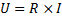
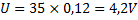
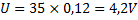
Om vi vet att totalspänningen är 
och även vet att spänningen över R1 är 
så kan vi räkna på spänningen över den parallellkopplade delen eftersom denna är seriekopplad med R1:
För seriekoppling gäller:
I vårt fall ger detta:
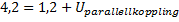
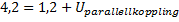
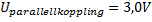
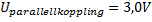
Spänningen över parallellkopplingen är 3,0V.
I en parallellkoppling är spänningen lika stor över alla grenar så spänningen över R4(som ingår i parallellkopplingen) är 3,0V.
Spänningen över R4 är 3,0V.
Nu har vi fått spänningen över R1 och R4, men R2 och R3 återstår.
I en parallellkoppling är:
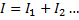
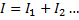
Eftersom vi vet att spänningen är 3,0V över R4 och att resistansen är 50 ohm kan sägas att strömmen genom denna del är:
Vi kallar denna ström för I1, och strömmen genom den andra grenen av parallellkopplingen för I2:
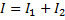
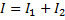
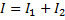
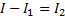
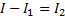
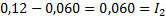
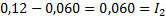
R2 och R3 är egentligen två seriekopplade resistorer där strömmen är 
.
Denna ström flyter genom bägge resistorerna och spänningen kan återigen räknas ut med Ohm´s lag:
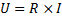
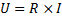
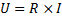
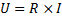
Spänningen över R2:
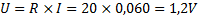
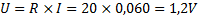
Spänningen över R3:
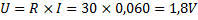
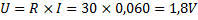
Svar: R1: 1,2V R2:1,2V R3:1,8V R4:3,0V
Polspänning och ems
Nu förstår vi att du antagligen är svintrött på resistanser och Ohm, och allt annat inom elläran men här kommer det sista! För din skull tar vi det lite kort och koncist.
Vi har hittills tittat på resistans ute i kretsen som gör att mindre ström går genom den. Nu ska vi titta på den resistans som finns i batteriet, den så kallade inre resistansen. Den inre resistansen(Ri) kommer att göra att batteriets spänning blir mindre.
Ju mer ström som går genom batteriet, desto större blir spänningsfallet enligt Ohm´s lag:
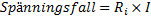
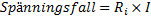
Polspänning kallar man den spänning som batteriet får efter spänningsfallet på grund av den inre resistansen.
EMS (elektromotorisk spänning) kallar man den spänning som faktiskt alstras på grund av kemiska processer i ett batteri. Om man sedan subtraherar spänningsfallet på grund av den inre resistansen får man polspänningen.
Detta kan skrivas såhär med ord:
Eller med fysikaliska beteckningar:
