Inledning
I kapitlet “Energi och Arbete” av Fysik 1 ska vi titta närmare på begreppet energi och i vilka former som energin kan förekomma. Som du säkert redan vet, finns det en massa former av energi (solenergi, vindenergi, rörelseenergi, kemisk energi m.m.) Ja, man kan faktiskt säga att allting som händer är resultat av energiomvandlingar!
Arbete
När vi i fysikens värld pratar om arbete menar vi inte när du står i kassan på Ica eller dylikt. Nej, här syftar vi egentligen på när något använder en kraft för att förflytta något. Säg exempelvis att du lyfter en väska 1 meter upp. När du gör detta säger man att du utför ett arbete.
Men hur stort blir arbetet? Man kan ju enkelt konstatera att det är jobbigare att lyfta en tyngre väska än en lättare. Det är även jobbigare att lyfta väskan 2 meter upp i luften än 1 meter. Dessa två faktorer bör alltså påverka hur stort arbetet blir. Det är också så att arbetet ökar med belastningen och förflyttningen enligt sambandet:
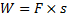
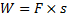
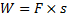
I denna formel (![]()
![]()
![]()
![]()
![]()
![]()
Enheten är Nm(newtonmeter) eller Joule(J) som är precis samma sak.
Exempel
Du lyfter en tjock bok på 2,0 kg rakt upp 1 meter. Hur stort arbete uträttar du?
Lösning
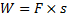
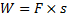
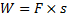
Boken väger 2,0 kg och har ungefär tyngden 20N(![]()
![]()


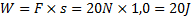
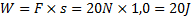
Svar: Arbetet är alltså 20J.
Så enkelt?
Nja, riktigt såhär enkelt är det inte alltid vid beräkningar med arbete. Nu tänker vi oss att du drar en vagn likt bilden nedan.


Vi ser i bilden att du påverkar vagnen med kraften F som kan delas upp i komposanterna F1 och F2. Det är nämligen bara den horisontella komposanten(F2) som uträttar ett arbete. Den vertikala komposanten är nämligen riktad vinkelrätt med rörelseriktningen, och därför utför den inget arbete.
Vi upprepar: Enbart krafter som är parallella mot rörelseriktningen utför ett arbete!
När du läst lite mer trigonometri (Matematik 4), så kommer ni lätt att kunna se att storleken av den horisontella komposanten är:
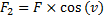
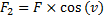
Arbetet får då sambandet:


Lägesenergi
I inledningen pratade vi om att allting som händer är energiomvandlingar. Här ska vi titta på en väldigt vanlig energiform som kan omvandlas, nämligen lägesenergin. Den beror, som namnet avslöjar, på läget! Ju högre upp ett föremål är, desto större är dess lägesenergi. När du exempelvis cyklar uppför en backe blir du trött för att den kemiska energin i dina muskler omvandlas till lägesenergi i och med att du kommer högre upp. Åker du sedan nedför backen förlorar du lägesenergi, men du får istället rörelseenergi då din fart ökar.
Vad påverkar lägesenergins storlek?
1. Man kan ju tänka sig att det kostar mer energi för en elefant att gå uppför en backe än det kostar dig. Därför bör en elefant få en större lägesenergi än du får när ni når backens topp.
2. Man kan även tänka säga att både du och elefanten får det jobbigare om backen är längre, och ni alltså kommer högre upp. Man borde få större lägesenergi om man kommer högre upp.
Det är faktiskt ovanstående två faktorer som påverkar lägesenergins storlek enligt formeln:




![]()
![]()
Nollnivå
För att kunna veta om något är högt upp eller långt ner bör man ha en nollnivå. Om vi sätter marken som nollnivå så är tallens topp väldigt högt upp. Om vi istället sätter Mount Everests topp som nollnivå är tallens höjd negativ!
Som tur är spelar det ingen roll var man sätter nollnivån då det är förändringar av lägesenergi som är intressanta. Det kostar nämligen lika mycket energi att lyfta något från 1 meter till 2 meters höjd som från 8 meter till 9 meters höjd.
Exempel
Du är på semester och klättrar i bergen. Du befinner dig 1500 meter över havet och ämnar nå toppen på 2100 meter. Vi säger att du väger 80 kg med utrustning och allt.
a) Vilken lägesenergi har du vid toppen, om nollnivån ligger vid havsytan?
b) Vilken lägesenergi har du vid toppen, om nollnivån ligger på 1500 meter över havet.
c) Hur ändras din lägesenergi under den sista bestigningen (1500-2100 meter)
Lösning
a) Vilken lägesenergi har du vid toppen, om nollnivån ligger vid havsytan?
Sträckan som du har förflyttat dig är 2100 meter.


Svar: Din lägesenergi ökar med ungefär ![]()
![]()
b) Vilken lägesenergi har du vid toppen, om nollnivån ligger på 1500 meter över havet.
Om nollpunkten ligger vid 1500 meters höjd är förflyttningen följande:
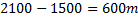
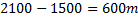


Svar: Lägesenergin blir då ![]()
![]()
![]()
c) Under sista etappen får vi den lägesenergi vi räknade ut i b) då du förflyttar dig 600 meter uppåt, det vill säga ungefär ![]()
![]()
![]()
Energiomvandlingar
I detta kapitel är det viktigt att man lär sig att förstå vilka energiomvandlingar som sker i vissa situationer, så här kommer några:
1. När bilen gasar omvandlas kemisk energi i bensinen till rörelseenergi som driver bilen framåt.
2. När du hoppar ner från en stol omvandlas lägesenergi till rörelseenergi.
3. När du klättrar uppför ett berg omvandlas kemisk energi i dina muskler till rörelseenergi, som i sin tur omvandlas till lägesenergi.
Rörelseenergi, även kallat kinetisk energi
Rörelseenergi är den energi som ett föremål har när det rör på sig. Som vi tidigare nämnt kan exempelvis lägesenergi omvandlas till rörelseenergi och tvärtom. När en boll exempelvis faller så kommer lägesenergi att omvandlas till rörelseenergi. När bollen når marken bör rimligtvis all lägesenergi ha blivit rörelseenergi.
Vad påverkar rörelseenergins storlek?
Två saker påverkar lägesenergins storlek:
1. Vi har tidigare lärt oss att ![]()
![]()
2. Dessutom borde ju rimligtvis farten hos föremålet som rör sig påverka rörelseenergin. En bil som kör snabbare bränner mer bensin, och får därför en större rörelseenergi.
I själva verket ser sambandet ut såhär:




I denna formel står ![]()
![]()
Energiprincipen
Energiprincipen är en av våra allra viktigaste fysikaliska lagar och går ut på att energi varken kan skapas eller förstöras, enbart omvandlas. Detta innebär att ”energiförluster” inte innebär att energi försvunnit, utan att energi omvandlats till en form som vi inte kan använda. Vi pratar då ofta om värmeenergi.
Att tillämpa energiprincipen
Det är alltid kul att kunna använda det man lär sig praktiskt, och det ska vi göra här!
Vi tänker oss att en sten faller fritt(utan energiförluster), från läge A till läge i bilden nedan:


Om vi sätter nollnivån vid läge B så har vi följande energisituation i de bägge lägena:
I läge A:







Här har stenen en lägesenergi, men ingen rörelseenergi då den saknar fart.
I läge B:







I detta fall har stenen ingen lägesenergi då den ligger vid nollnivån, men däremot har den en rörelseenergi då den har en fart.
Enligt energiprincipen kan ingen energi ha försvunnit och:


Eller:



Lägesenergin i läge A har alltså helt omvandlats till rörelseenergi i läge B.
Exempel
Nu har du klättrat upp i hopptornet på badhuset. Hopptornet är fem meter högt och du känner dig ytterst osäker på om du vågar hoppa. Därför vill du självklart veta vilken fart du kommer att ha när du slår i vattnet. Hur stor är denna fart?
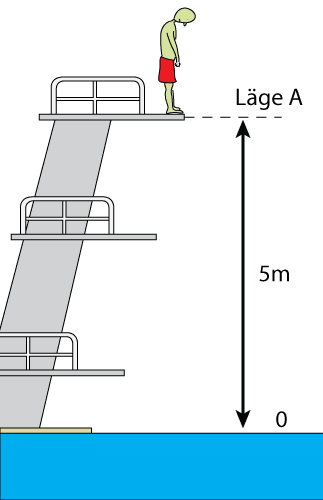

Lösning
I läge A:







Här har du en lägesenergi, men ingen rörelseenergi då du står stilla.
I läge B:







Enligt energiprincipen är:



Vi kan dividera bägge sidor med (m) och får då:






Om höjden(h) är 5 meter så gäller:


Svar: Hastigheten när du når vattnet är ungefär 36 km/h!
Observera att det inte spelade någon roll hur stor massan på det fallande föremålet var i föregående exempel.
Kaströrelse
Genom att använda energiprincipen kan man också räkna på en kaströrelse. En kaströrelse kommer till en början vara en energiomvandling från rörelseenergi till lägesenergi. Sedan når man dock en topp och det man kastar börjar gå ner mot marken. Då kommer lägesenergi istället att omvandlas till rörelseenergi.
Enligt energiprincipen är dock totalenergin i varje läge konstant.


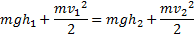
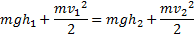
Exempel
Du kastar en sten enligt kastbanan nedan.


a) Hur stor fart har stenen i banans högsta punkt?
b) På vilken höjd över utgångspunkten är farten 7 m/s?
Lösning
a) Hur stor fart har stenen i banans högsta punkt?
I utgångspunkten (Läge A) har vi ingen lägesenergi men en rörelseenergi.
Totalenergi i läge A:



I den högsta punkten (läge B) har vi en viss rörelseenergi och en lägesenergi:
Totalenergi i läge B:


Enligt energiprincipen är totalenergin i läge A lika med totalenergin i läge B:


Återigen kan vi nu dividera båda led med (m) och få:


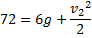
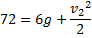
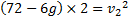
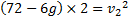


b) På vilken höjd över utgångspunkten är farten 7 m/s?
I utgångspunkten(Läge A) har vi ingen lägesenergi men en rörelseenergi.
Totalenergi i läge A:



På den höjd där farten är 7 m/s(läge C) har vi en lägesenergi och en rörelseenergi:




Totalenergin i läge C är:


Enligt energiprincipen är totalenergin i läge A lika med totalenergin i läge C:


Vi dividerar som tidigare båda led med (m):


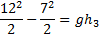
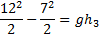
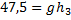
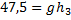


Svar: På ungefär 4,8 meters höjd är farten 7 m/s.

