Inledning
I kapitlet “Rörelse” för Fysik 1 kommer vi att titta på läge, rörelse och tid. Vi kommer utgå ifrån vad som för dig kanske är gammal kunskap, och sedan bygga på detta med lite nya roligheter! Vi kommer att lära oss att beskriva rörelsen när en boll kastas upp i luften, och även beskriva rörelse längs en bana (exempelvis: bilens rörelse när familjen drar på fjällsemester).
Likformig rörelse
En likformig rörelse har en konstant hastighet. Det är den likformiga rörelsen som du säkert har stött på tidigare, främst i matematik 1 som “svt-formeln“:



I ovanstående formeln står (s) för sträckan (förflyttningen), (v) för hastigheten och (t) för tiden. Allt mäts självfallet i SI-enheter som är meter, meter per sekund och sekunder.
Genom en omskrivning av ovanstående formel kan man få:
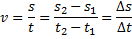
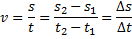
En förklaring av ovanstående är att hastigheten är lika med förflyttningen dividerat med tiden förflyttningen tar. Beteckningen delta (
Exempel
Lastbilschauffören Lasse kör från Karlstad till Kristinehamn. Sträckan mellan städerna är 45 km och det tar honom 40 minuter. Hur snabbt kör han?
Lösning









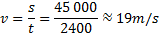
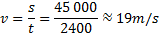
Svar: Han håller ungefär hastigheten 19 m/s.
Läge-tid-graf
En läge-tid-graf har sträckan på y-axeln och tiden på x-axeln. Med denna kan man se förflyttningen hos ett föremål under ett visst tidsintervall. Nedan visas en läge-tid-graf.


I bilden ovan har vi en likformig rörelse, vilket alltså betyder att hastigheten är konstant. Detta ger en rätlinjig graf.
Vi vet sedan tidigare att:
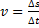
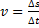
Vi provar nu i bilden att mäta förändringen i y-led (sträckan eller ![]()
![]()
![]()
![]()
Momentanhastighet och medelhastighet
När ni sitter i bilen på väg mot fjällen kanske det tar 2 timmar att köra 200 km. Enligt formeln i föregående avsnitt kommer då hastigheten att vara 100 km/h. Det är ju dock inte troligt att ni har legat och kört exakt 100 km/h hela tiden, hastigheten varierar säkert under dessa två timmar. Dock så kommer medelhastigheten att vara 100 km/h.
Vi kan alltså konstatera att formeln ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Om vi sedan mäter medelhastigheten under en väldigt kort tidsperiod så får man i princip hastigheten i ett visst ögonblick. Hastigheten i ett visst ögonblick kallas för momentanhastigheten.
Momentanhastigheten kan utläsas från sträcka-tid-grafen genom att läsa av kurvans lutning i en viss punkt, se bilden nedan:


S = vt?
Vi har hittills lärt oss att ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Du har just köpt dig en ny Ferrari och vill självklart testa vad den går för. Du vill helt enkelt veta hur snabb din nya kärra är. Du undersöker detta genom att dra med två kompisar ner till “Autobahn” och ställer upp dem med 1000 meters mellanrum. Den förste får en signalpistol och den andre får ett tidtagarur. Din geniala plan är att du ska bränna förbi den första kompisen i full fart varvid han skjuter pistolen. När den andra kompisen hör pistolen startar han tidtagaruret som stoppas när du kör förbi honom. Då menar du att ni med hjälp av ![]()
![]()
![]()
![]()
![]()
![]()
![]()
Problemet är att du kör så himla fort att pistolen skjuts av lite försent, vilket gör att tidtagaruret startas lite försent. Bilen har hunnit 100 meter när tidtagaruret startas och alltså faller hela beräkningen.
I sådana här tillfällen krävs en utvidgning av formeln:
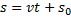
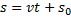
I denna formel är ![]()
![]()
![]()
Om ni inte förstod det något långsökta exemplet så kan man kort sagt säga att sträcka och tid är två relativa begrepp. Om du springer ett hundrameterslopp är starten satt till nollpunkt(s=0). Om du startar när startskottet går kommer ![]()
![]()
![]()
![]()
Såhär ser läge-tid-grafen ut när ![]()
![]()
![]()
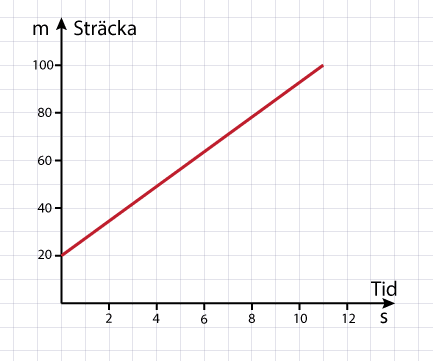

Notera att y är större än noll när x är lika med noll.
Hastighet-tid-graf
Hittills har vi tittat på hur sträckan förändras med tiden. Vi har konstaterat att hastigheten är lutningen hos sträcka-tid-grafen samt att ![]()
![]()
Bilden nedan visar en hastighet-tid-graf:
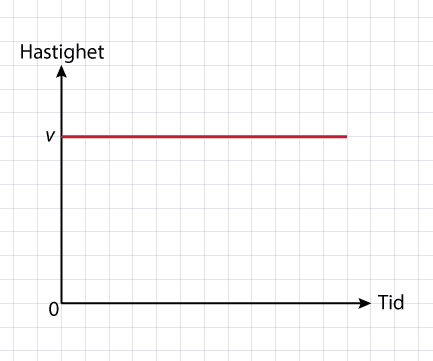

Bilden visar hastigheten hos en likformig rörelse jämfört med tiden. Som vi förväntar oss är linjen rak eftersom hastigheten är konstant hos en likformig rörelse.
En mycket intressant sak med bilden ovan är att det ganska enkelt går att multiplicera hastigheten och tiden, genom att välja ett tidsintervall. Då får vi enligt ![]()
![]()
![]()
![]()
![]()
![]()
![]()


Arean under hastighet-tid-grafen är lika med sträckan föremålet rör sig under tidsintervallet! Observera att detta gäller oavsett om hastigheten är konstant(likformig rörelse) eller varieras(icke-likformig rörelse).
Exempel
Du kör din Ferrari i 288 km/h. Du får höra på radion om en olycka 1000 meter framför dig och ställer dig självklart på bromsen. Inbromsningen visas i hastighet-tid-grafen nedan. Hinner du stanna innan olyckan?


Lösning
I bilden ser vi att inbromsningen tar 15 sekunder. Hastigheten är från början 80 m/s(288km/h). Vi vet att arean under grafen är sträckan som bilen hinner förflytta sig under de 15 sekunderna, alltså bromssträckan.
Arean bildar en triangel och kan räknas ut på följande vis:


Svar: Bromssträckan är 600 meter och du kan alltså pusta ut hela 400 meter framför olyckan!
Acceleration
Återigen sitter du i din Ferrari. Du kör lugnt och fridfullt när en stöddig typ i en Porsche glider upp vid din sida. För att visa var skåpet ska stå trampar du på gasen och har på några få sekunder ökat din hastighet från 80 km/h till 200 km/h. Du har accelererat!
En acceleration är alltså när ett föremål förändrar sin hastighet över tid. Notera att accelerationen kan vara negativ om hastigheten sänks(Ferrarin bromsar). En negativ acceleration brukar dock kallas för en retardation.
Accelerationen kan alltså beskrivas med följande formel:


Nu ska vi titta på vilken enhet accelerationen kan tänkas få. Hastighet har enheten m/s och tid har enheten sekunder.
Om vi dividerar:
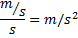
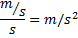
Enheten är alltså ![]()
![]()
Momentanacceleration och medelacceleration
Tidigare i denna sammanfattning tittade vi på medelhastighet och momentanhastighet och dessa är väldigt lika de två begrepp vi nu ska prata om.
Medelaccelerationen är helt enkelt den genomsnittliga accelerationen under en hastighetsförändring. Accelerationen kan variera under tidsperioden men den genomsnittliga accelerationen(medelaccelerationen) kan räknas ut med formeln:


Momentanaccelerationen är accelerationen i ett visst ögonblick. Denna fås genom att man tittar på accelerationen i ett väldigt kort tidsintervall. Man kan även få ut momentanaccelerationen ur en hastighet-tid-graf genom att titta på lutningen i en viss punkt enligt bilden nedan:
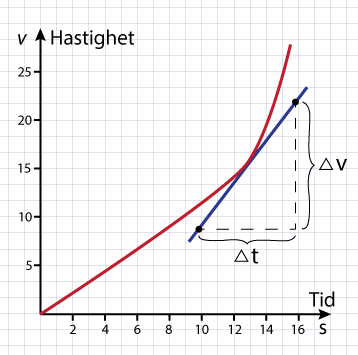

Likformig accelererad rörelse
Förut tittade vi på en likformig rörelse som hade en konstant hastighet och därför fick en linjär sträcka-tid-graf. En likformig rörelse har en konstant hastighet och därför ingen acceleration eller retardation. En likformig accelererad rörelse har istället en konstant acceleration.
Fritt fall!
Eftersom du är en riktig adrenalinnarkoman har du nu anmält dig till att hoppa fallskärm. På vägen upp börjar du dock bli lite skakis och tänker tankar som ”tänk om fallskärmen inte vecklas ut”. Du fattar ändå mod och kastar dig ut. Du faller till en början handlöst och din hastighet ökar snabbt. Sedan vecklas din fallskärm ut och du bromsar in kraftigt. Skönt!
Nu ska vi titta lite närmare på den första delen av fallskärmshoppet, nämligen den fritt fallande delen. Om vi bortser från luftmotståndet så finns det bara en kraft som påverkar dig när du faller utan fallskärm, och det är tyngdkraften. Tyngdkraften är konstant och även den acceleration (tyngdaccelerationen) som påverkar dig.


I denna formel är tyngdfaktorn(g) 9,82 och tyngdaccelerationen är faktiskt precis lika stor, nämligen 9,82 m/s2!
Gränshastighet
Nu efter hoppet kanske du funderar på vad som skulle ha hänt om inte fallskärmen skulle ja utvecklas. Till en början hade då din rörelse i princip varit likformigt accelererad. Men efter ett tag hade accelerationen minskat mer och mer för att slutligen upphöra vid den ungefärliga hastigheten 60 m/s. Detta beror på att luftmotståndet blir större med högre hastighet och vid ungefär 60 m/s är den lika stor som tyngdkraften. Då påverkas du inte av någon kraft längre och hastigheten förblir konstant.
Det är ovanstående fenomen som gör att en fjäder faller långsammare än ett bowlingklot. En fjäder har en väldigt liten massa jämfört med volym, vilket gör att dess tyngdkraft lätt uppnås av luftmotståndet och den har en låg gränshastighet. Ett bowlingklot har däremot en hög massa jämfört med volym och därför påverkas den av en stor tyngdkraft. För att luftmotståndet ska bli lika stort som tyngdkraften så måste bowlingklotet uppnå en högre hastighet. Gränshastigheten är alltså större.
Notera att fjädern och bowlingklotet faller precis lika fort i vakuum där inget luftmotstånd finns.
Ett par formler
Hastighet
Slutligen ska vi titta på några formler som kan vara vettiga att kunna räkna med.
Först tittar vi på hastigheten för en likformigt accelererad rörelse:





Ovanstående formel betyder helt enkelt att hastigheten är lika med ursprungshastigheten (![]()
![]()
![]()
![]()
![]()
![]()
Sträcka
Det finns ett par formler som man kan räkna med vid beräkning av sträckan om rörelsen är likformigt accelererad.
Formel 1 (observera den fyndiga språkleken, racingbilen, jättekul)
Vid en likformig rörelse sade vi att sträckan var lika med hastigheten multiplicerat med tiden(![]()
![]()
![]()
![]()
![]()
![]()
![]()
Medelhastigheten är:
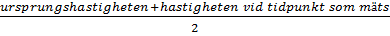
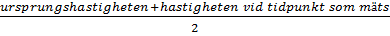
eller kort och gott:
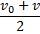
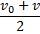
Likt (![]()
![]()
![]()
![]()
![]()
![]()
![]()



Formel 2
Tidigare i sammanfattningen har nämnts att sträckan är arean under hastighet-tid-grafen. Detta är självklart ingen slump! Du kanske har läst lite om derivata (Matematik 3). Hastigheten är i alla fall sträckans derivata, dvs. om man deriverar formeln för sträcka så får man formeln för hastighet.
Nu ska vi prova att derivera baklänges formeln för hastighet som vi redan lärt oss:





Med regler som ni glatt kommer lära er i Matematik D kan man då säga att:


Ovanstående är alltså den andra formeln för sträckan hos ett föremål som utför en likformigt accelererad rörelse.
Exempel 1
Mor Stina spatserar stolt med sin son Gustav i en barnvagn. Plötsligt kommer en nedförsbacke och mor Stina tappar till sin förskräckelse taget om barnvagnen och Gustav åker iväg med en allt högre fart. I början av backen har barnvagnen hastigheten 5 km/h och längst ner i backen är hastigheten 18 km/h. Färden tar 10 sekunder.
a) Hur stor är accelerationen under färden nedför backen?
b) Hur lång är backen?
Lösning
a)
Först ska vi göra om hastigheterna till SI-enheter:
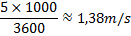
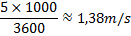
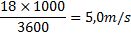
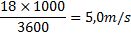
Nu räknar vi ut accelerationen:


Svar: Accelerationen är ungefär ![]()
![]()
b)







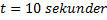
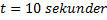
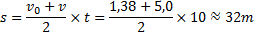
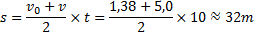
Svar: Backen är 32 meter lång!
Exempel 2
Gustav överlevde vagnfärden i förra exemplet och har nu blivit intresserad av sten. Han tar en sten och kastar den rakt upp i luften med hastigheten 15 m/s. Tyngdaccelerationen kan sägas vara
10 m/s2.
a) Vilken hastighet har stenen efter 2,0 sekunder?
b) Hur högt når stenen?
c) Var befinner sig stenen efter 2,0 sekunder?
d) När är stenen tillbaka vid utgångspunkten?
e) Vilken hastighet har stenen när den är tillbaka vid utgångspunkten?
Lösning
a) Vilken hastighet har stenen efter 2,0 sekunder?
För det första kan vi konstatera att tyngdaccelerationen är den enda accelerationen som påverkar stenen. Den är riktad nedåt och alltså negativ om positiv riktning sätts uppåt.













Svar: Hastigheten är ![]()
![]()
![]()
b) Hur högt når stenen?
När stenen vänder är dess hastighet 0 (![]()
![]()
Först måste vi räkna ut vid vilken tidpunkt stenen vänder:







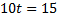
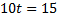


Tiden är alltså 1,5 sekunder.
Nu ska vi titta på hur högt stenen når:


Svar: Stenen når 11 meter upp i luften, Gustav är med andra ord en hejare på att kasta sten!
c) Var befinner sig stenen efter 2,0 sekunder?
I deluppgift (a) konstaterade vi att hastigheten vid tidpunkten 2,0 sekunder var ![]()
![]()
![]()


Svar: Stenen är 10 meter upp i luften vid tidpunkten 2,0 sekunder.
d) När är stenen tillbaka vid utgångspunkten?
När stenen är tillbaka vid utgångspunkten är sträckan 0 meter.


När sträckan är noll gäller att:


Bryt ut (t):


Med nollproduktsmetoden (se vår Matematik B-sammanfattning!) får man att:
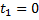
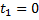
Annars är


Då är ![]()
![]()
Svar: Stenen kommer ner igen efter 3,0 sekunder.
e) Vilken hastighet har stenen när den är tillbaka vid utgångspunkten?





Vi har i föregående deluppgift räknat ut att tiden är 3,0 sekunder.
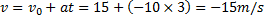
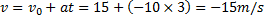
Svar: Hastigheten är -15m/s, alltså 15m/s riktad mot marken.

