Vad är densitet och tryck? Och varför behöver man veta det? Läs denna sammanfattning av Fysik 1 så förklarar vi!
Inledning
Har du någon gång sett en fakir sitta på sin spikmatta? Han sitter på spikar utan att få en skråma! Du kanske också har funderat över vad dykarsjuka innebär, eller varför man ibland får ont i öronen när man flyger flygplan. Dessa är några av frågorna som du kommer att kunna svara på efter att ha läst detta kapitel!
Tryck mellan fasta kroppar
När fakiren sitter på spikmattan kommer ett tryck att uppstå mellan två fasta kroppar, nämligen spikarna och fakirens skinkor. Vi ska nu undersöka av vilka faktorer som trycket påverkas. Vi börjar med att tänka lite intuitivt:
- Man kan logiskt tänka sig att en tyngre fakir kommer att få ondare än en lättare fakir. Alltså bör tyngden påverka trycket.
- Dessutom kan man tänka sig att det gör ondare att sitta på en spik än att sitta på tusen spikar.
Det är faktiskt bara dessa två faktorer som påverkar trycket mellan fasta kroppar.
Lite mer formellt kan man sammanfatta detta med formeln:



P motsvarar trycket och mäts i enheten N/m2 eller enheten Pascal (Pa).
Så varför kan fakiren sitta?
Nu ska vi svara på ursprungsfrågan. För det första kan man säga att en fakir ofta är ganska benig och har således en liten vikt. Detta ger en liten tyngdkraft (F). Dessutom så sitter fakiren på väldigt många spikar, vilket ger en stor tvärsnittsarea (A). Om vi hade tagit bort ett antal spikar så hade han grinat illa!
Exempel
Nu ska vi prova att räkna på tryck!
Vi har hästen Stella som står på marken och betar. Hur stort tryck utövar en hov mot marken om Stella väger 600 kg och en hov har tvärsnittsarean 4x2cm2 ?
Lösning
Stellas tyngd är:
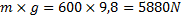
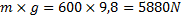
Stella utövar kraften 5880N med fyra hovar. Med en hov utövar Stella kraften:


Kraften F är 1470N.
Tvärsnittsarean A är enligt uppgiften 4,0 x 2,0 = 8,0 cm2. Men man ska alltid räkna med SI-enheter i fysik, vilket i detta fall är meter. Därför skriver vi om i kvadratmeter på följande vis:




En kvadratmeter motsvarar alltså tiotusen kvadratcentimeter.


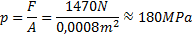
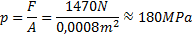
Svar: Varje hov utövar trycket 1,8 MPa på marken.
Densitet
Densitet har vi redan beskrivit tidigare i sammanfattningen. Du kan nå förklaringarna om densitet genom att klicka HÄR.
Vätsketryck
Nu lämnar vi fakiren för ett tag och går istället till en dykare. Du har säkert hört talas om att en dykare utsätts för ett stort tryck när han går ner några tiotal meter i vattnet. Detta beror på vätsketrycket. Om dykaren efter att ha varit nere på djupt vatten går upp till ytan för fort finns risken att han drabbas av dykarsjukan. Dykarsjukan får han för att tryckförändringen blir för stor på för kort tid.
Detta är bara ett exempel på när man måste ha med vätsketrycket i beräkningarna. Vi kommer i detta avsnitt att lära oss mer om vätsketryck och om hur vi kan använda vätsketrycket i vardagen.
Lite intuitivt!
Vi börjar återigen lite intuitivt:
- Här kan man tänka sig att trycket blir större ju längre ner man kommer i vattnet. Vi får inte dykarsjukan av att dopa huvudet under vattnet, men vi kan få dykarsjukan av att gå ner 40 meter och sedan återvända upp för fort.
- Påverkar tvärsnittsarean? När det handlade om trycket mellan fasta kroppar så gav en större total tvärsnittsarea ett lägre tryck. I vattnet skulle man då få tänka sig att det skulle ge ett större tryck att dyka i en stor sjö kontra i en liten sjö, och detta stämmer inte! Tvärsnittsarean påverkar alltså inte vätsketrycket.
Med dessa två tankar i bagaget ska vi nu fortsätta vår resa mot insikt i hur man räknar på vätsketrycket!
Lite fakta
Här kommer lite fakta mer fakta om vätsketrycket:
- Som vi tidigare har sagt blir trycket större på större djup.
- Det är vätskemolekylerna som ger trycket.
- På djupt vatten kommer vi få ont i öronen för att molekylerna slår mot trumhinnorna.
- Vätsketrycket beror enbart av djupet, alltså inte av tvärsnittsarean.
Räkna på vätsketrycket
Man kan räkna på vätsketrycket med följande formel:
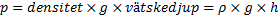
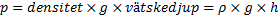
Med denna formel kan man räkna på vätsketrycket men om man vill ha det totala trycket som exempelvis påverkar en dykare så måste man ta vätsketrycket och addera det med lufttrycket.
Alltså:


Några exempel
Exempel 1
Maja dyker ner 25 meter i sjön Vänern. Hur stort vätsketryck påverkas hon av?
Lösning
Djupet (h) är 25 meter.
Gravitationskonstanten (g) är som alltid 9,8 N/kg.
Densiteten för vatten är 1000kg/m3.


Svar: 250 000Pa (Observera att detta inte är det totala trycket som Maja påverkas av då hon även påverkas av lufttrycket).
Exempel 2
I figuren nedan finns vatten och olja i ett U-rör. Vad är oljans densitet?


Lösning
För att lösa denna uppgift måste man inse att om man skulle trycka på i ena hålet av U-röret så skulle vätskan stiga i andra hålet. Vi ser i figuren att den del av U-röret som delvis innehåller olja har vätskeytan högre upp än den del som enbart innehåller vatten. Detta innebär att vatten har en högre densitet än olja då det rena vattnet uppenbart trycker upp den del som innehåller olja.
Trycket kommer att vara lika högt i båda delarna av röret på samma nivå. Vid den streckade linjen börjar skiktet av olja. Skiktet av olja är 5,0 cm. Om vi drar en streckad linje, enligt figuren över till andra delen av U-röret så ser vi att vätskedjupet där är 4,6 cm. Vi kan alltså konstatera att 5,0 cm olja ger samma tryck som 4,6 cm vatten.
Med ovanstående fakta kan vi börja räkna:
Vätsketrycket i den del av röret som enbart innehåller vatten är:
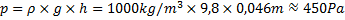
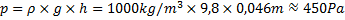
5 centimeter olja kommer ge samma tryck och därför kan vi säga att:


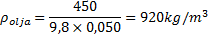
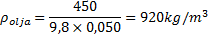
Exempel 3
Nedan har vi två kärl med olika bottenytor. Den ena har radien 10,0 centimeter och den andra har radien 5 centimeter. Vattendjupet är 7 centimeter i bägge kärlen. Beräkna trycket i de bägge kärlen.


Lösning
Detta är ju en kuggfråga! Radien spelar ingen roll för vätsketrycket. Det är således lika stort i bägge kärlen då vätskedjupet är lika stort.
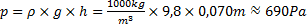
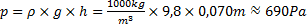
Svar: Trycket är i botten på bägge kärlen ungefär 690 Pa
Kuriosa
Vätsketryck kan användas för att generera enorma krafter i exempelvis en domkraft, men detta får du läsa mer om i din fysikbok!
Gastryck
Hittills har vi sett hur tryck kan påverka en fakir och dykaren Maja. Nu tittar vi istället på Bob som ska flyga flygplan. När planet lyfter och stiger uppåt märker Bob att han får ont i öronen. I detta avsnitt ska vi bland annat undersöka varför Bob får ont i öronen.
Ett experiment
Vi lägger en kokosboll (med vitt skum i, typ mums-mums) i en vakuumpump. Vakuumpumpen pumpar ut all luft ur behållaren så att det bildas något som liknar vakuum. Detta gör att kokosbollen exploderar!
Hur förklarar vi detta tragiska öde?
I vanliga fall kommer det finnas ett gastryck i kokosbollen (som innehåller mycket luft) och ett gastryck utanför kokosbollen. Gastrycket i kokosbollen kommer att trycka kokosbollen utåt medan gastrycket utanför kokosbollen kommer att trycka den inåt. Dessa två krafter kommer dock i vanliga fall att ta ut varandra och nettokraften blir noll, vilket gör att kokosbollen behåller sin form.
När vi med vakuumpumpen pumpar ut luft ur behållaren där kokosbollen ligger så sjunker trycket utanför kokosbollen. Då blir krafterna som trycker ihop kokosbollen mindre. Lufttrycket inuti kokosbollen förändras dock inte vilket gör att krafterna som trycker kokosbollen utåt blir större än krafterna som trycker kokosbollen inåt och den exploderar. Det blir ruskigt kladdigt!
Mer om lufttryck
- Likt vätsketrycket beror på att vätskemolekylerna rör sig så beror gastrycket på att gasmolekylerna rör sig.
- Vårt normala lufttryck ligger på ungefär 101,3kPa, vilket motsvarar en vattenpelare på ungefär 10 meter.
- Lufttrycket mäts med en barometer.
- Lufttrycket kommer att sjunka ju högre upp man kommer. Detta gör att det blir svårt att bestiga Mount Everest. När lufttrycket sjunker, sjunker även syrgastrycket vilket gör att man får syrgasbrist.
Barometern
En barometer fungerar genom att man har en vätska som är i kontakt med en gas. Om gastrycket ökar så kommer vätskan att pressas uppåt i det rör som den befinner sig i. Genom att mäta höjden av vätskepelaren kan man då avgöra hur stort gastrycket är.
Vi sade förut att det normala lufttrycket motsvarar en vattenpelare på ungefär 10 meter. Detta innebär att en barometer med vatten skulle ha behövt vara tio meter hög, vilket inte skulle vara så praktiskt. Kvicksilver har en mycket högre densitet. En kvicksilverpelare på 760 mm motsvarar faktiskt normalt lufttryck. Därför är det fördelaktigt att använda kvicksilver i barometrar.
Ett exempel på en barometer med kvicksilver visa nedan. Observera att den fungerar precis som det tidigare exemplet med vatten och olja i ett U-rör. Istället för att vattnet pressar upp olja så pressar ett högt lufttryck upp kvicksilvret.
Några exempel
Exempel 1
I en ångpanna har vi trycket 0,30MPa. Hur stor är kraften mot ångpannans ändyta om ändytan har arean 0,80m2?
Lösning
Eftersom det här handlar om en tryckkraft från gasen som pressar mot en fast yta så kan man använda formeln:



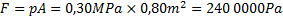
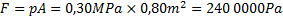
Svar: Tryckkraften mot behållarens ändyta är 240 N.
Exempel 2
Du sitter i ett flygplan på 11 500 meters höjd. Lufttrycket är här 21kPa utanför, medan det inuti kabinen är 83kPa. Kabinfönstret med arean 4,5 dm2 kommer då att utsättas för en kraft på grund av tryckskillnaden utanför och innanför flygplanet. Hur stor blir denna kraft?
Lösning:
Nettotrycket är:
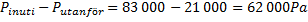
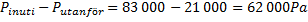
Arean är 4,5 dm2 som i kvadratmeter blir 0,045 m2.
Enligt formeln för tryckkraft mot en fast yta ger detta:


Svar: Tryckkraften på fönsterrutan blir 2800 N riktad utåt.
Viktigt!
I vätska kunde vi ju räkna på vätsketrycket med formeln:
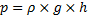
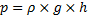
Denna formel fungerar även för gaser men problemet blir att densiteten blir olika vid olika höjder. Om densiteten skulle ha varit lika stor olika högt upp så hade trycket stigit ju högre upp i atmosfären man kom, vilket vi vet inte är sant.
I vätska räknar vi med att densiteten är konstant vid olika vätskedjup.
Arkimedes princip
På dagis fick vi prova att lägga en bit bark i vattnet. Den flöt vilket var väldigt roligt, men vi reflekterade inte särskilt mycket över varför den flöt. Men det ska vi göra nu!
I tidigare kapitel har vi lärt oss att tyngdkraften påverkar alla föremål med massa. Tyngdkraften kommer att dra föremål ner mot marken. Barkbiten måste ju också påverkas av tyngdkraften och alltså borde den falla mot botten i vattnet, men det gör den ju inte!
Vi har två tänkbara förklaringar till ovanstående fenomen:
- Tyngdkraften verkar inte på föremål i vatten. Denna förklaring är dock rätt kass eftersom en sten kommer att sjunka till botten väldigt snabbt och således påverkas av tyngdkraften.
- Vi har någon sorts kraft som motverkar tyngdkraften och trycker föremålet uppåt.
Det är alltså förklaring nummer två som stämmer och denna kan förklaras med Arkimedes princip.
Formellt lyder principen såhär
”Lyftkraften på ett föremål i en vätska är lika stor som tyngden av den vätskemängd som föremålet tränger undan.”
En förenklad version
Ett föremål i en vätska kommer att tränga undan en del vatten (vattennivån höjs när du går ner i badkaret). Den vätskemängd som trängs undan har en viss tyngd. Denna tyngd kommer att vara lika stor som vattnets lyftkraft på föremålet.
Varför flyter träbiten?
En träbit har en mindre densitet än vatten. Den vätska som träbiten tränger undan har alltså en större tyngd än själva träbiten. Vätskans tyngd är samma som vätskans lyftkraft på träbiten. Lyftkraften blir då större än tyngdkraften på träbiten och vi får en resulterande kraft uppåt som gör att träbiten flyter.
Att räkna med Arkimedes
Det finns en formel som man kan använda som ser ut på följande vis:
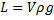
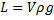
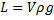
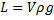
Detta är egentligen enbart en formel som beskriver samma saks om Arkimedes princip gör i ord. Med denna formel ska vi i nedanstående exempel räkna på träbiten i vattnet!
Exempel
Med dina nyvunna kunskaper vill du självklart räkna på barkbiten som råkar väga 0,18kg.
a) Hur stor är lyftkraften på barkbiten i vatttnet?
b) Hur stor volym vatten tränger barkbiten undan?
Lösning
a)
De två krafter som påverkar barkbiten är dels tyngdkraften på den som är riktad neråt, och lyftkraften på den som är riktad uppåt. Eftersom barkbiten flyter så måste dessa två krafter vara lika stora.


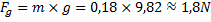
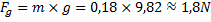
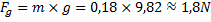
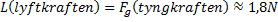
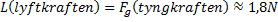
Svar: Lyftkraften är alltså ungefär 1,8N
b)
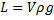
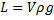
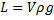
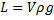
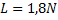
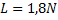
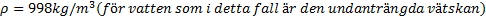
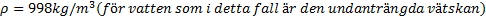




Svar: Barkbiten tränger undan ungefär 0,18 liter vatten.
Gasers lyftkraft
Nu vet vi alltså varför träbiten flyter i vattnet. En annan sak många av er säkert har provat är att köpa en heliumballong. Det roliga med en heliumballong är att den flyger iväg om man släpper den, och nu ska ni få se att även detta är en konsekvens av Arkimedes princip som även fungerar för gaser!
Gaser har dock mycket mindre densitet än vätskor, vilket gör att gasers lyftkraft blir mycket mindre.
I en heliumballong kommer själva ballongen (gummit) att påverkas av tyngdkraften neråt. Helium har dock densiteten 0,18 kg/m3 jämfört med luftens 1,3kg/m3. Detta gör att ballongen även kommer att påverkas av en lyftkraft uppåt. Om ballongen är tillräckligt uppblåst med helium så kommer lyftkraften att överväga tyngdkraften och ballongen lyfter.
Exempel
Du har fått en enorm heliumballong med volymen 1,0 m3. Helium har densiteten 0,18kg/m3 (vid jordytan).
a) Hur stor är lyftkraften på ballongen?
b) Hur stor är den resulterande kraften på ballongen?
c) Hur stor måste ballongen vara för att kunna lyfta dig?
Lösning
a)
Enligt Arkimedes princip är:
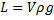
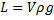
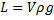
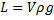
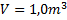
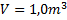
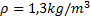
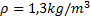
(observera att vi använder densiteten för luft i formeln då det är luft som trängs undan och alltså genom Arkimedes princip ger en lyftkraft)
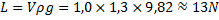
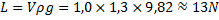
b)
Den resulterande kraften är differensen mellan lyftkraften på ballongen (riktad uppåt) och tyngdkraften som påverkar ballongen (riktad neråt).
Lyftkraften (FL) är ju som vi redan konstaterat ungefär 13N.
Tyngdkraften på ballongen:


Ballongens massa (m) är massan av heliumgasen (vikten av själva gummit bortser vi ifrån). Massan av heliumgasen är volymen heliumgas multiplicerat med densiteten för helium enligt sambandet:




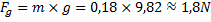
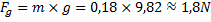
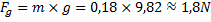
Den resulterande kraften(FR) räknas således ut på följande vis:
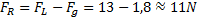
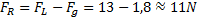
Den resulterande kraften på ballongen är alltså ungefär 11N riktad uppåt.
c)
Vi har förstås ingen aning om vad du väger men vi kan ta en annan rolig typ som exempel.
Nicke Nyfiken får i ett avsnitt en heliumballong av mannen med den gula hatten. Problemet är att ballongen lyfter och flyger iväg med Nicke. Vi vet inte vad Nicke väger men vi säger att han väger
5,0 kg.
Vi vet nu att en heliumballong med volymen 1 m3 påverkas av den resulterande kraften 11N uppåt. För varje m3 man ökar ballongvolymen kommer alltså lyftkraften att öka med 11N.
Det som motverkar den resulterande kraften på ballongen är i detta fall tyngdkraften som påverkar Nicke. Denna räknas ut såhär:
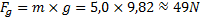
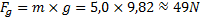
Den resulterande kraften på ballongen måste alltså vara större än 49N för att ballongen ska lyfta Nicke.
Om den resulterande kraften på ballongen ökar med 11N per m3 så kan man göra följande beräkning:
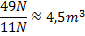
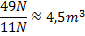
Slutsatsen är alltså att mannen med den gula hatten måste ha gett Nicke en väldigt stor ballong!

