Inledning
I begynnelsen av denna kurs (avsnitt 1 “Kraft“för Fysik 1 pratade vi grundläggande om krafter. Vi tittade på gravitationen, normalkrafter och andra krafter som verkar i samma riktning eller precis motsatt riktning. Nu ska vi utöka våra kraftkunskaper till att kunna hantera “krafter åt alla håll”, dvs. situationer där krafterna verkar i flera olika riktningar. Vi kommer också att fundera över hur en gungbräda fungerar samt varför tjuven kan använda en kofot till att bända upp dörren.
Tips: Detta avsnitt innehåller lite grundläggande trigonometri (Matematik 4) så om det är främmande rekommenderas att du tar en titt på den länken.
Tips: Studera Smart! Vissa av uppgifterna i din lärobok är ordentligt kluriga kring dessa ämnen/kapitel. Du bör därför inte lägga alltför mycket tid på de svåraste delarna i din kursbok, då det antagligen kommer 1-2 stycken uppgifter från detta kapitel på nationella provet. Du ska dock självklart kunna de flesta uppgifterna, och vi har därför tagit med några exempel som vi tycker är bra.
Kraftkomposanter
Att sätta ihop olika krafter
Redan i kapitel 3 pratade vi om att man kunde ersätta flera krafter med en resulterande kraft. Vi ska spinna vidare på detta.
I bilden nedan har vi Stina och Pelle som släpar en sten genom att dra i varsitt rep. Nedan är kraftriktningarna ritade:
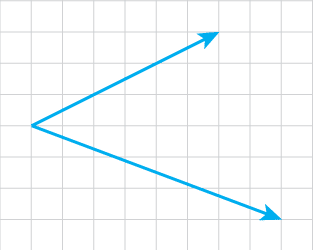

Nu ska vi se om vi kan få ihop dessa krafter till en gemensam resulterande kraft. Du gör detta genom att rita en kraftparallellogram:
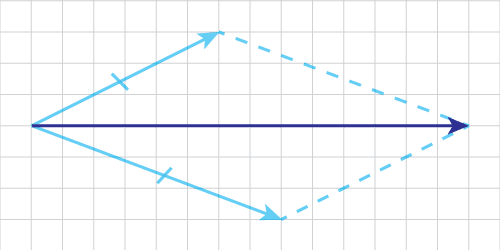

Vi kallar de krafter som Stina och Pelle drar med(de som vi sedan sätter ihop till en resulterande kraft) för kraftkomposanter.
Att dela upp i kraftkomposanter
På motsvarande vis kan man dela upp en kraft i dess kraftkomposanter genom att dela upp kraften i en vertikal komposant och en horisontell komposant. Vi visar med bilden nedan:




Exempel 1
Gör ett exempel där kraftkomposanter ska delas upp i resulterande kraft
Lösning
Svara på uppgiften
Svar: Svara på uppgiften om du har några värden på krafterna
Exempel 2
Gör ett exempel där en resulterande kraft ska delas upp i kraftkomposanter.
Lösning
Svara på uppgiften
Svar: Svara på uppgiften om du har några värden på krafterna
Exempel 3 (svårare men viktigt)
Glada Gustav åker skidor nedför en backe med lutningen 20 grader. Han väger med utrustning 50 kg. Bestäm normalkraften och friktionskraften. Gustav varken ökar eller minskar sin fart och vi räknar inte med luftmotståndet.


Lösning
Det kluriga med den här uppgiften är egentligen att bena ut vilka krafter som påverkar den glade Gustav och hur dessa är riktade. Vi vet att tyngdkraften påverkar honom precis rakt ner och vi vet att denna kraft är på ungefär 500N(![]()
![]()


Observera att tyngdkraften är riktad rakt ner mot jordens medelpunkt, alltså inte vinkelrätt med backen. Tyngdkraften kommer att göra två saker; dra Gustav nerför backen, och dra Gustav mot underlaget. Detta kan visas genom att dela upp tyngdkraften i komposanter:


Som ni ser drar den vertikala kraftkomposanten(F1) Gustav ner mot marken. Eftersom han inte sjunker genom marken måste det finnas en lika stor motriktad kraft som drar honom uppåt. Detta är normalkraften. Kraftkomposanten F1 är alltså lika stor som normalkraften.
Den horisontella kraftkomposanten(F2) kommer att dra Gustav nedför backen, men eftersom han håller en konstant hastighet måste det finnas en motriktad kraft som bromsar honom. Detta är friktionskraften. Kraftkomposanten F2 är alltså lika stor som friktionskraften.
Med lite trigonometri som vi inte går in på här så kan man få fram att om backens lutning är 20 grader så är även vinkeln mellan tyngdkraften och dess kraftkomposant F2 20 grader, enligt bilden:


Nu kan vi med rätt enkel trigonometri få att:


Friktionskraften är lika stor som F1, alltså ungefär 170N


Normalkraften är som redan nämnt lika stor som F2, alltså ungefär 470N.
Svar: Friktionskraften är ungefär 170N och normalkraften är ungefär 470N.
Kraft och arbete
Nu kommer ännu ett begrepp som vi är bekanta med sedan tidigare, nämligen arbete (Energi inom Fysik 1)
Först kommer en repetition av vad arbete är, sedan ska vi fördjupa oss lite.
När vi i fysikens värld pratar om arbete menar vi inte när du står i kassan på Ica eller dylikt. Nej, här syftar vi egentligen på när något använder en kraft för att förflytta något. Säg exempelvis att du lyfter en väska 1 meter upp. När du gör detta säger man att du utför ett arbete.
Men hur stort blir arbetet? Man kan ju enkelt konstatera att det är jobbigare att lyfta en tyngre väska än en lättare. Det är även jobbigare att lyfta väskan 2 meter upp i luften än 1 meter. Dessa två faktorer bör alltså påverka hur stort arbetet blir. Det är också så att arbetet ökar med belastningen och förflyttningen enligt sambandet:


I denna formel (![]()
![]()
![]()
![]()
![]()
![]()
![]()
Enheten är Nm(newtonmeter) eller Joule(J) som är precis samma sak.
Nytt om arbete
Tidigare har vi titta på arbete när kraften som utför arbetet har precis samma riktning som förflyttningen. Nu tänker vi oss istället att kraften är i en lite annan riktning, vi visar detta nedan.
I bilden nedan drar lilla Olle på sin fina vagn. Han har ett rep som han drar vagnen med och kraften han drar med har samma riktning som repet.


Nu ska vi titta på hur stort arbete Olle utför när han drar vagnen. Vi har ju tidigare sagt att ett arbete endast utförs om kraften är riktad parallellt med rörelseriktningen. Vi kan dela upp Olles kraft på vagnen i en vertikal och en horisontell komposant. Den horisontella komposanten är riktad åt samma håll som vagnen rör sig, och det är denna kraft som utför ett arbete.


Exempel
Nu tittar vi på hur stort arbetet blir. Vi säger att Olle drar vagnen enligt figuren nedan. Hur stort arbete uträttar han om han drar vagnen 100 meter på plan mark.
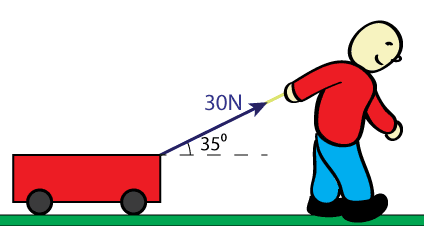

Lösning


Vi delar först upp kraften i komposanter och kan med trigonometri räkna ut den horisontella komposantens(FH) storlek:
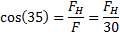
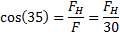


Sträckan Olle drar vagnen är 100 meter.


Svar: Han uträttar ett arbete på 2500J.
Kraftmoment
Nu ska vi äntligen titta på varför tjuven kan bända upp en dörr med kofot, hur gungbrädan fungerar och hur du med ett simpelt spett kan flytta på stora stenar. Det gemensamma för alla dessa situationer är att något vrider sig. Det kan vara dörren, axeln som gungbrädan står på eller stenen. Kraftmomentet ger denna vridning, vilket vi nedan kommer att se.
Vi ska börja med att tänka oss följande scenario:
Det var en rysk, en tysk och en Bellman som skulle se vem som var starkast. För att göra detta skulle de flytta på en sten. Ryssen och tysken försökte lyfta stenen men kunde inte rubba den. Sedan kom Bellman! Han drog fram ett spett och kunde utan problem bända bort stenen genom att köra in spettet under den.
Detta kanske inte var den mest fyndiga Bellman-vitsen, men den tjänar väl som exempel på kraftmoment. Rent intuitivt kan man tänka sig att ju längre ut Bellman håller på spettet desto lättare blir det att flytta stenen. Detta beror på att spettet blir en hävarm. En längre hävarm kommer att göra att vi får ett större kraftmoment. Kraftmomentet gör att stenen vrider sig och rullar bort. Stenen rullar runt sin vridningsaxel.
Oj, nu blev det lite mycket på en gång, vi reder ut begreppen igen:
1. Kraftmomentet ger föremålet den påverkar en förmåga att vrida sig. Ju större kraftmoment, desto hellre vill föremålet vridas. Bellman fick stenen att vridas (rulla).
2. Vridningsaxeln är den axel ett föremål vrider sig runt när det roterar. Om du öppnar en dörr kommer gångjärnen att vridas så att hela dörren vrids. Då är gångjärnen vridningsaxeln.
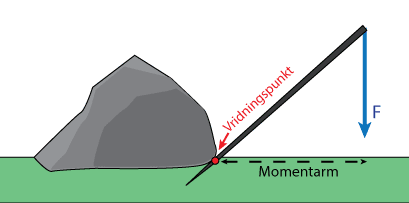
3. Hävarmen är avståndet från kraften som påverkar föremålet, till föremålets vridningspunkt. I Bellmans fall är det raka avståndet från den punkt där spettet påverkar stenen(vridningspunkten) till den punkt där Bellman trycker ner spettet med sina händer.

Formeln för kraftmoment är:


I denna formel står (![]()
![]()
(![]()
![]()
![]()
![]()
![]()
Exempel
Ange kraftmomentet som Bellman lyckas uppnå i den situation vi har nedan:


Lösning
Kraften är 800N. Det vi måste ta reda på är hu lång momentarmen blir. Vi gör detta genom att dela in längden av spettet i en horisontell och en vertikal komposant enligt bilden nedan:
Det är den horisontella längdkomposanten i bilden som utgör hävarmen eftersom detta är det kortaste avståndet från vridningspunkten till kraften.
Med trigonometri kan man få att denna är:
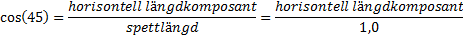
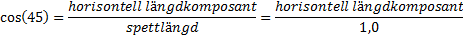


Okej, om hävarmen är ![]()
![]()
![]()
![]()


Notera att man aldrig använder enheten Joule när man pratar om kraftmoment då detta begrepp är något helt annat än energi.
Rotationsjämvikt
Nu har vi tittat på hur stenen kan flyttas och ska raskt gå vidare till gungbrädan. När du var liten kanske det hände att din pappa gungade med dig på gungbrädan. Ni kunde gunga fastän han var mycket tyngre och borde göra att du är fast upp i luften. För att undvika denna ytterst beklagliga situation väljer din pappa då att använda kraftmomentet och sätta sig längre in på gungbrädan. Ju längre in han sätter sig, desto mer faller din del av gungbrädan ner. I ett visst läge är ni bägge i luften. I detta läge har ni uppnått rotationsjämvikt.
Bäst att vi reder ut begreppet rotationsjämvikt. När du och din pappa gungar på gungbrädan kommer ni att påverka vridpunkten på gungbrädan med varsitt motriktat kraftmoment. Vid rotationsjämvikt kommer era kraftmoment att vara lika stora och gungbrädan kommer ligga helt still.
Hur går detta till?
Din pappa väger mer än dig, men eftersom han sitter närmare gungbrädans vridpunkt kommer hans hävarm att bli kortare. Detta gör att ni påverkar gungbrädan med lika stora kraftmoment, fastän olika riktade. Detta kan skrivas med en formel:
![]()
![]()
![]()
![]()


Exempel
Vi ska nu räkna på gungbrädor och annat skoj. Du och din pappa gungar alltså på brädan enligt figuren nedan. Hur långt ifrån gungbrädans mittpunkt ska din pappa sitta om ni ska uppnå rotationsjämvikt?
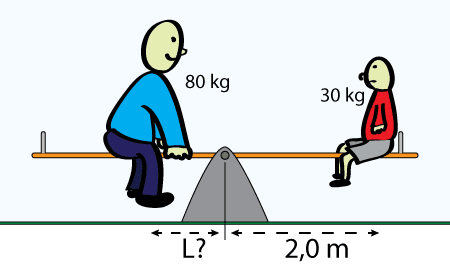

Lösning
Vi börjar med att titta på de kraftmoment som du och din pappa påverkar gungbrädan med.
Du påverkar den med:






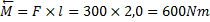
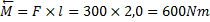
Du påverkar brädan med kraftmomentet 600Nm.
Din pappa påverkar den med:








Din pappas kraftmoment på brädan är ![]()
![]()
Vid rotationsjämvikt gäller att:
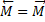
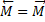
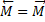
Alltså är:




Svar: Din pappa ska sitta 0,75m från brädans mittpunkt, eller vridningspunkt.
Translationsjämvikt
Nu vet vi hur en gungbräda fungerar, en fantastisk insikt som retar nyfikenheten! Vi lämnar dina barndomsår, och du har växt upp till din nuvarande ålder. Du och din pappa umgås fortfarande men den här gången ska ni istället snickra. Ni ska såga av en lång planka och lägger den på två bockar. Då slår tanken dig att det kanske är någon sorts jämvikt som har uppkommit, och så är det! Plankan har uppnått translationsjämvikt!
Vi ska reda ut detta begrepp med bilden nedan:


Som vi ser i bilden ligger brädan stilla på sina bockar. Detta tyder på att krafterna som påverkar den tar ut varandra. Krafterna är tyngdkraften som verkar från brädans tyngdpunkt och de två normalkrafterna som verkar på brädan från bockarna. Detta ger translationsjämvikt.
Translationsjämvikt är när alla krafter som påverkar ett föremål tar ut varandra. I exemplet ovan tar normalkrafterna ut tyngdkraften.
Vi kan dock konstatera en sak till i exemplet ovan, nämligen att det råder rotationsjämvikt eftersom plankan inte roterar. Kraftmomenten måste alltså vara lika stora åt bägge håll.
Jämviktsvillkor
1. Alla krafter måste ta ut varandra. Resultanten är alltså 0.
2. Det råder rotationsjämvikt, vilket innebär att kraftmomenten tar ut varandra.
Exempel
Detta exempel är taget direkt från fysikboken Heureka! och är numrerad som 11.21.
Beräkna krafterna, som bockarna utövar på brädan i figuren, om brädan väger 7,1kg.
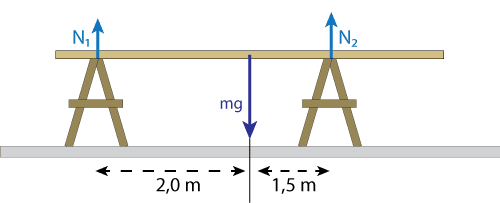

Lösning
Vi söker efter normalkrafterna(N1 och N2). Eftersom det råder translationsjämvikt vet vi att:


Dessutom vet vi att det råder rotationsjämvikt eftersom brädan inte rör sig:
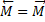
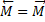
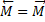
Detta kan också skrivas som att:


Nu kan vi sätta ihop ett fint ekvationssystem:


Vi kan skriva om ekvation (1) till:
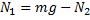
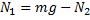
Nu ersätter vi ![]()
![]()
![]()
![]()
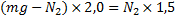
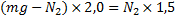
Nu gör vi lite omskrivningar:
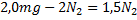
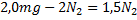


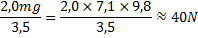
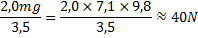
Vi ersätter ![]()
![]()
![]()
![]()
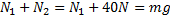
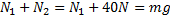


Svar: Den vänstra bocken utövar normalkraften 30N på brädan medan den högra utövar normalkraften 40N på brädan.

