Krafter är ett begrepp som uppfanns redan på slutet av 1600-talet, genom att ett äpple trillade ner på Isac Newtons huvud! I detta avsnitt ska vi djupdyka i begreppen krafter och rörelse.
Inledning
I detta sista kapitel av fysik 1 ska vi prata väldigt mycket om den fantastiske vetenskapsmannen Sir Isaac Newton, eller snarare om hans fantastiska upptäckter inom fysiken som faktiskt lade grunden till det vi idag kallar för den klassiska fysiken. Vi ska med andra ord spinna vidare på kraftbegreppet och lära oss mer om friktion, gravitation, normalkrafter med mera.
Tips: Titta på kapitlet krafter samt kapitlet om rörelse längs en bana, då vi kommer att bygga vidare på resonemang som presenteras i dessa två kapitel.
Tröghetslagen – Newtons första lag
Tröghetslagen är egentligen Newtons första lag. För att beskriva denna tänker vi oss att du sitter i bilen. Du har ställt in bilens farthållare och du håller alltså en jämn hastighet. Bilen färdas alltså i en likformig rörelse. I detta läge verkar följande krafter på bilen:
I detta läge kommer:
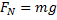
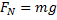
Med ord kan man säga att normalkraften från vägen på bilen och tyngdkraften måste ju ta ut varandra eftersom bilen inte går genom marken. Dessutom måste den accelererande kraften vara lika stor som friktionskraften eftersom bilen varken ökar eller minskar sin hastighet.
Vi kan konstatera att vi inte har några resulterande krafter, och detta liknar verkligen en annan situation som vi har pratat om tidigare, nämligen föremål i vila.
När en bok ligger på ett bort påverkas den av två krafter: tyngdkraften från jorden samt normalkraften från bordet. Dessa krafter tar ut varandra och boken är i vila. Newton insåg också denna likhet och formulerade därför sin tröghetslag på följande vis:
”Varje kropp förblir i vila eller likformig rörelse om den inte av krafter tvingas att ändra sitt rörelsetillstånd.”
Med enklare ord kan man säga att detta innebär att om alla krafter tar ut varandra(vilket är fallet i vila och likformig rörelse) kommer föremålet som rör sig inte att ändra sin hastighet. Om vi däremot tillför en ny kraft, exempelvis att vi gasar mer med bilen kommer vi ha en resulterande kraft framåt som gör att bilen accelererar.
Om bilen sedan bromsar in kraftigt kommer du att tryckas framåt. Detta beror på att ingen bromsande kraft har påverkat dig, även om en sådan har påverkat bilen. Därför fortsätter du i samma hastighet som innan ända tills bilbältet tar emot och utövar en bromsande kraft på dig.
Kraftekvationen – Newtons andra lag
Nu har vi alltså konstaterat att det behövs en kraft för att ändra ett föremåls rörelse, men hur stor är denna kraft?
Newton funderade över detta också och han började säkert, likt vi ska börja, att tänka rent intuitivt.
1. Man kan tänka sig att en större kraft kommer att ge en större acceleration, och en mindre kraft kommer att ge en mindre acceleration. Om vi återgår till din bil så kommer accelerationen bli större om du trampar gasen i botten, jämfört med om du mestrampar på gasen.
2. Dessutom kan man tänka sig att det krävs en större kraft för att få en tung lastbil att accelerera jämfört med en lätt motorcykel. Alltså bör föremålets massa tas med i beräkningarna.
Det är faktiskt dessa två faktorer som helt avgör hur stor accelerationen blir då formeln ser ut på följande vis:
Detta brukar oftast skrivas om på formen:
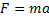
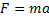
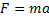
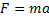
Exempel 1
Motorerna i en Boeing 747 utvecklar en framåtdrivande kraft på 
. Maximala totala vikten för planet är 
.
a) Vad är den maximala accelerationen för planet innan det lyfter?
b) Vilken hastighet har planet efter 10 sekunder?
Lösning
a) Vad är den maximala accelerationen för planet innan det lyfter?
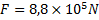
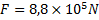
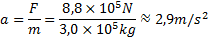
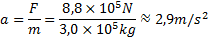
b) Vilken hastighet har planet efter 10 sekunder?
Nu tar vi till gamla kunskaper för likformigt accelererad rörelse:
I vårt fall har vi ingen ursprungsfart då planet startar från stillastående, alltså är 
Vi får:
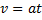
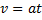
Med accelerationen 
och tiden 10 sekunder ger detta:
Svar: 29m/s eller 104km/h
Exempel 2
En motorcykel accelererar från 30km/h till 120km/h på 5 sekunder. Motorcykeln väger 200 kg inklusive förare.
a) Beräkna accelerationen
b) Beräkna sträckan som passeras när motorcykeln accelererar
c) Beräkna det arbete som den totala kraften framåt gör
d) Beräkna den resulterande kraften på motorcykeln
Lösning
a) Beräkna accelerationen
Ursprungshastigheten 
är 
eller cirka 
.
Sluthastigheten 
är 
eller cirka 
Tiden är 5 sekunder.
Gammal kunskap är att:
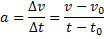
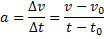
Med våra värden ger detta:
Svar: Accelerationen är 
.
b) Beräkna sträckan som passeras när motorcykeln accelererar
Gammal kunskap är att:
Med våra data får vi att:
Svar: Sträckan som passeras när motorcykeln accelererar är ungefär 100 meter.
c) Beräkna det arbete som den totala kraften framåt gör
Kraften som orsakar accelerationen kan räknas ut med kraftekvationen:
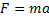
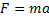
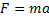
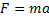
Vi har tidigare räknat ut (
) till .
Massan är 
enligt uppgiften.
Sedan tidigare vet vi att följande gäller för arbete:
I b) räknade vi ut att sträckan var 100 meter.
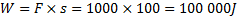
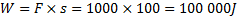
Svar: Det uträttade arbetet är ungefär 
.
d) Beräkna den resulterande kraften på motorcykeln
Svar: Vi har ju redan räknat ut i c) att den resulterande kraften på motorcykeln(den accelererande kraften) är 
!
Kraftekvationen vid fritt fall
Du kanske redan har reflekterat över att kraftekvationen är väldigt lik formeln för beräkning av tyngdkraften.
Kraftekvationen:
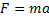
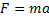
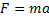
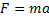
Beräkning av tyngdkraften:
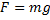
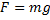
Att falla fritt är en likformigt accelererad rörelse eftersom kraften på det som faller är konstant och man kan faktiskt skriva:
Dividerar vi sedan med (
) så får vi att:
Accelerationen vid fritt fall och tyngdfaktorn är alltså samma sak!
Kraftekvationen om flera krafter verkar
Det finns tyvärr många situationer där det inte går att försumma friktionen som vi annars så glatt gör när vi räknar. Låt oss återgå till din bil. Du sitter och kör på motorvägen och kör fort när du plötsligt lägger bilen i friläge och låter den rulla. Då kommer det inte dröja särskilt länge innan bilen tappar fart och stannar. Här kan vi alltså definitivt inte räkna bort friktionen. Vi tittar på bilden nedan:
Vi ser att den framåtdrivande kraften F1 är större än friktionskraften F2, alltså kommer bilen att accelerera. Friktionskraften är dock så stor att vi måste räkna med den.
Den accelererande kraften kommer då att bli:
Vi måste alltså i dessa fall modifiera kraftekvationen till:
Exempel
Du accelererar med din bil genom att gasa så att den drivande kraften blir 
. Hur stor blir accelerationen om friktionskraften är 
och bilen väger 
?
Lösning
Först räknar vi ut den accelererande kraften:
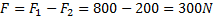
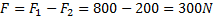
Sedan använder vi kraftekvationen som säger att:
För oss ger detta att:
Svar: Accelerationen blir 
.
Rörelselagarna och energiresonemang
Ofta kan det vara smart att använda energiresonemang för att lösa rörelseproblem och vi kommer här att visa ett par sådana exempel.
Exempel 1
Du kastar en boll rakt upp med hastigheten 
. Hur högt når den?
Lösning 1
Först löser vi den på vanligt vis med rörelselagarna.
När stenen når sin högsta punkt kommer den att vända. Då är hastigheten 
, och vi vill nu veta vid vilken tidpunkt detta inträffar.
Formeln för hastighet när det gäller likformigt accelererad rörelse lyder:
I vårt fall är accelerationen tyngdfaktorn, som alltså blir 
om positiv rörelseriktning sätts uppåt.
är för oss .
I vändläget när stenen når sin högsta punkt gäller att 
.
Genom omskrivningar får vi att:
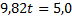
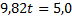
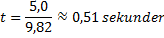
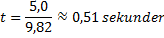
Sedan vet vi också att:
När bollen vänder kommer formeln att se ut såhär:
Svar: Stenen når ungefär 1,3 meter upp över den punkt du kastade den ifrån.
Lösning 2
Nu ska vi istället lösa uppgiften med energiresonemang!
Då kan man säga att den rörelseenergi som stenen hade när den lämnade handen kommer helt att ha omvandlats till lägesenergi när stenen når sin högsta punkt(om vi bortser från friktionsförluster).
Alltså gäller att:
Vi förkortar lite:
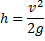
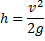
Med våra siffror ger detta:
Svar: Stenen når ungefär 1,3 meter upp över den punkt du kastade den ifrån.
Exempel 2
En gevärskula som väger 10 gram har hastigheten 400m/s. Kulan träffar en sandsäck och stannar 3 cm in i säcken. Beräkna kraften på kulan inne i säcken genom att:
a) Använda ett energi-arbete-resonemang
b) Använda rörelselagarna och kraftekvationen
Lösning
a) Använda ett energi-arbete-resonemang
Vi kan tänka oss att den rörelseenergi som kulan har när den susar in i säcken kommer att omvandlas till värmeenergi när kulan bromsar in på grund av att ett arbete utförs. Arbetet utförs av den bromsande kraften som säcken har på kulan.
Vi kan med andra ord säga att:
Eller att:
Med omskrivning ger detta att:
Om vikten är 10 gram(0,010kg), hastigheten är 400m/s och bromssträckan är 0,03m så gäller:
Svar: Den bromsande kraften blir ungefär 
.
b) Använda rörelselagarna och kraftekvationen
Nu ser vi istället på situationen som en rörelse som har bromsat in från hastigheten 
till hastigheten 
.
Denna inbromsning sker på sträckan 0,03 meter.
Vi ska nu ta reda på under vilken tid inbromsningen sker, genom att använda formeln:
Med omskrivningar ger detta:
Med våra data får vi då:
Vidare vet vi att:
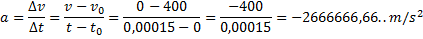
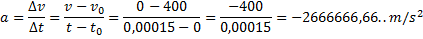
Observera att accelerationen är negativ för att det är en inbromsande rörelse.
Kraftekvationen ger sedan:
Svar: 
, minustecknet finns där för att det är en bromsande rörelse.
Referenssystem
Vi kan uppleva olika situationer på olika vis genom att vi befinner oss i olika referenssystem. Om du sitter i bilen och kör så tycker du att bilar du möter kör väldigt fort. Om du kör i 100km/h och bilen som möter dig kör i 100km/h upplever du att du möter en bil som kör i 200km/h. Detta sker för att ni är i olika referenssystem.
Samma sak gäller när du tvärnitar med bilen. Då kommer du flyga framåt på grund av att du fortfarande är i ett referenssystem som rör sig med en konstant hastighet, medan bilen är i ett referenssystem som rör sig med en retarderande hastighet. Du trycks då framåt för att du påverkas av en så kallad tröghetskraft. Denna kraft finns inte på riktigt och kallas därför för en fiktiv kraft, men du kan uppleva den ändå!