XYZ
Detta är ett nytt delprov inom högskoleprovet som testar dina kunskaper inom några matematiska områden. I delen XYZ ska du räkna fram ett svar till skillnad från delen NOG där du bara ska bedöma om den givna informationen räcker för att lösa uppgiften eller ej. Det finns 24 stycken uppgifter och dessa är meningen att du ska lösa på 24 minuter. Här tänkte vi lära dig hur du löser alla dessa uppgifter utan problem, så hugg in!
Uppgifterna är utformade såsom att det ställs en matematisk fråga och fyra svarsalternativ varav ett av dessa alternativ är rätt.
Nog snackat, nedan kommer lite fakta om olika uppgiftstyper som kan komma inom XYZ.
Högskoleprovet (XYZ) - Aritmetik
Aritmetiken är den grundläggande räknekonsten. Under denna rubrik ingår addition, subtraktion, division och multiplikation.
Några termer som är bra att kunna:
- Vid addition och subtraktion får man en summa
- Vid multiplikation får man en produkt
- Vid division får man en kvot
Dessutom brukar man dela in tal i olika grupper:
- Naturliga tal är alla positiva heltal
- Heltal är alla positiva och negativa heltal
- Rationella tal är alla positiva och negativa heltal plus alla bråk
- Reella tal är alla positiva och negativa heltal, alla bråk och alla tal som inte kan skrivas som bråk, typ.
Exempel
Skoj, då kan vi lite mattespråk! Här kommer en exempeluppgift:
Tre direkt på varandra följande ojämna tal har summan 27. Vad blir deras produkt?
A) 53
B) 123
C) 504
D) 693
Lösning
Okej, först måste vi se vilka tre tal det är frågan om. Om det var samma tal skulle det vara 9. 9+9+9=27. Nu ska det vara tre på varandra följande udda tal. Vi tar därför istället 9 och dess två udda grannar 7 och 11.
7 + 9 + 11 = 27
Summan av dessa tre är sedan:
7 * 9 * 11 = 693
Svar: D
Högskoleprovet (XYZ) - Bråk
Bråk har som ni vet en täljare överst, sedan ett bråkstreck och en nämnare underst, typ: Bråk har som ni vet en täljare överst, sedan ett bråkstreck och en nämnare underst, typ:
Addition och subtraktion av bråk
Vad som kan vara kul är att förlänga och förkorta bråk så att de får samma nämnare. Detta gör man när man vill addera eller subtrahera bråk:
Ovanstående tal kan skrivas om som:
Som ni ser ovan har vi förlängt 
med fyra så att nämnaren blir åtta i bägge fallen. Sedan är det bara att lägga ihop de båda täljarna, schysst va!
Multiplikation av bråk
Här är det bara att multiplicera täljarna och nämnarna, inga konstigheter.
Division av bråk
Här vänder man först på det bråk som man delar med och sedan kör man multiplikation av täljarna och nämnarna:
Ser ni att vi bara vänt på 
till 
och sedan multiplicerat som vanligt.
Exempel
Här kommer ett exempel från provet ht-2011:
Vilket svarsförslag är lika med 
?
B)
C)
D)
Lösning
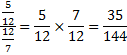
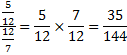
Svar: A
Högskoleprovet (XYZ) - Potenser
En potens är när ett tal är upphöjt i något. Talet som upphöjs kallas för bas, och det man upphöjer i kallas för exponent. Detta innebär att talet multipliceras med sig själv det antal gånger som talet är upphöjt i, alltså:
Tal kan också vara upphöjda i något negativt, men det blir inte så mycket krångligare:
Tal med negativ bas
Nu tittar vi istället på negativa tal som upphöjs. Här gäller samma sak som förut, men det kan vara lite klurigt att komma fram till om svaret är negativt eller positivt. Huvudregeln är att om exponenten är ett jämnt tal så blir svaret positivt, medan om exponenten är ett negativt tal så blir svaret negativt.
Exempel
18 är ett jämnt tal och alltså blir svaret 1.
17 är ett ojämnt tal och därför blir svaret -1.
På motsvarande vis blir: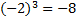
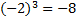
medan 
Att räkna med potenser
Nu ska vi räkna lite med potenser.
Multiplikation
Om bägge talen som man ska multiplicera har samma bas (i detta fall 5) så kan man bara addera exponenterna för att få produkten. Observera att detta inte fungerar om talen har olika baser.
Division
När man delar tal som har samma bas kan man på motsvarande vis subtrahera exponenterna.
Högskoleprovet (XYZ) - Algebra
Algebra är när man blandar in bokstäver och andra symboler i matematiken.
Ett typiskt algebraiskt uttryck är: 
Nu ska vi titta närmare på hur man löser ut x i olika situationer, vilket brukar vara en allmänt populär högskoleprovuppgift.
Addition och subtraktion
Multiplikation
Det kan bli lite krångligare om det handlar om parenteser. Här multiplicerar vi ihop två parenteser: 
Det här är faktiskt enklare än det ser ut, det är bara att utföra multiplikationerna var för sig:
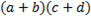
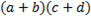
Addera bråk
Vakna till nu för detta är rätt bra att kunna! Vi ska lära oss att addera och subtrahera olika bråktal.
Hemligheten bakom denna fina konst är att man har samma nämnare i de bägge bråken man tänker addera eller subtrahera.
Okej, om vi ska kunna addera ihop dessa två bråk måste vi först ha en gemensam nämnare. Vi får detta genom att multiplicera 3x med 2 och 2x med 6.
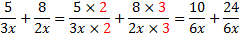
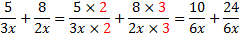
Observera att vi måste multiplicera både täljare och nämnare med talet för att det ska bli rätt.
Nu har vi den gemensamma nämnaren 6x för de bägge bråken, och då är det bara att addera täljarna så är vi klara:
Att lösa ekvationer
Nu kan vi dividera bägge sidor med 5 och få ut x:
Ett annat exempel är tvärtom:
Nu kan vi istället multiplicera bägge sidor med 5 och lösa ut x:
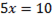
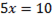
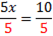
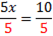
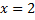
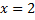
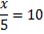
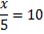
x = 50 Korsmultiplikation
De två reglerna ovan gör att man kan använda något som kallas för korsmultiplikation.
Om vi exempelvis har att:
Så kan man tänka sig att vi vill lösa ut x. Då använder vi korsmultiplikation som går till såhär:
Notera att vi har multiplicerat diagonalt vilket innebär att vi har multiplicerat det ena bråkets täljare med det andra bråkets nämnare.
Sedan är det inte så svårt att lösa ut x.
Så vi dividerar bägge sidor med 20: 
Detta ger att:
Exempel
Vad är x om:
A) 6
B) 12
C) 18
D) 24
Lösning
Okej, vi ser att talen på vänstersidan redan har samma nämnare, då kan vi slå ihop dessa:
Då vet vi att:
Genom att sedan multiplicera bägge sidor med x får vi:
Sedan dividerar vi bägge sidor med 0,5 och får:
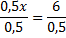
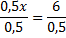
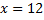
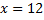
Svar: B
Som ni förstår måste man nöta en del ekvationer innan reglerna sitter. Ni hittar mer information om ekvationer HÄR.
Högskoleprovet (XYZ) - Funktioner
Funktioner är beskrivet väldigt bra i vår kurshjälp så vi föreslår att du spanar in den HÄR.