Geometri har använts i tusentals år i alltifrån byggnadsplanerande till avståndsuppskattning och till och med i Einsteins relativitetsteori. Det är med andra ord rätt bra att lära sig!
På den sida går vi igenom grundläggande begrepp inom geometri för att du ska kunna ta dig igenom Matematik 1 på gymnasiet.
Innehåll – Geometri:
1. Omkrets och area
2. Omkrets och area för cirkel
3. Rätblock, prisma och cylinder
4. Begränsningsyta och mantelarea
5. Klot och kon
6. Vinklar
7. Vinkelsumma
8. Trianglar
9. Skala
10. Proportionering
11. Likformiga trianglar
12. Pythagoras sats
1. Omkrets och area – Geometri
Genom att rita flera sträckor kan man skapa en geometrisk figur. Ett sådant exempel är en rektangel, vilken består av fyra punkter, s.k. hörn, mellan vilka det dras fyra sträckor. Dessa sträckor kallas för sidor, uppdelade i bredd och längd. Summan av sidornas längder kallas rektangeln omkrets.
För rektangeln gäller att vinkeln mellan två sidor i ett hörn är rät (90°) och att motstående sidor (dvs. sidor mitt emot varandra) är parallella samt lika långa.


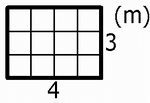
Ovanstående rektangel har längden 4 m och bredden 3 m.
Omkretsen 3 + 3 + 4 + 4 = 14 m.
Rektangeln utgör en begränsad yta. Storleken på ytan kallas area. För att ange arean används areaenheter. En vanlig areaenhet är kvadratmeter (skrivs m2). Arean (A) för en rektangel beräknas genom att multiplicera längd (l) och bredd (b) och det kan skrivas med hjälp av en formel:


För ovanstående rektangel är arean A = 4 • 3 = 12 m2

Ovanstående areaformel motiverar varför areaenheten är m2. Genom att multiplicera l och b kan man säga att längdenheterna ”m” och ”m” multipliceras. Därmed fås m • m = m2.
1 m2 kan ses som en kvadrat (rektangel med lika långa sidor) där varje sida är en meter lång. Eftersom 1 m = 100 cm så är varje sida 100 cm. För att ange arean uttryckt i cm2 så används areaformeln ovan:
A = 100 • 100 = 10 000 cm2
Observera här skillnaden mellan längd och area vid s.k. enhetsomvandling:
1 m = 100 cm 1 m2= 10 000 cm2
Då decimaltecknet flyttas två steg vid omvandling av längdenheter så flyttas det dubbelt så många steg, fyra steg, vid omvandling av areaenheter.
Några vanliga areaenheter:


Dessutom förekommer:
1 a (”ar”) = 100 m2
1 ha (”hektar”) = 10 000 m2
1 ha = 100 a
2. Omkrets och area för cirkel – Geometri
Då vi ska räkna ut omkretsen och arean för en cirkel måste vi använda oss av konstanten π, som uttalas ”pi”. Ett närmevärde med tre gällande siffror för är 3,14 och med fem gällande siffror blir det 3,1416. De flesta miniräknare har dock en särskild knapp för och då föreslår jag att du använder den istället. Detta för att få ett så exakt svar som möjligt, och det är bättre att avrunda endast i slutet istället för att göra det redan från början. Då är risken att få fel svar större.
För att räkna ut omkretsen för en cirkel så tar vi diametern multiplicerat med π. Diametern är det bredaste stället på cirkeln, man drar ett streck från cirkelns kantlinje, genom mittpunkten och sen fram till stället mittemot det man började. Diametern är samma sak som radien multiplicerat med 2.


Omkretsen för en cirkel är: ![]()
![]()
![]()
![]()
Arean av en cirkel får vi genom att multiplicera π med radien i kvadrat. Radien är halva diametern, det vill säga avståndet från mittpunkten till cirkelns kant.
Arean för en cirkel är: ![]()
![]()
3. Rätblock, prisma och cylinder
Rätblock
Ett rätblock begränsas av rektanglar. Ett rätblock har sex sidoytor, åtta hörn och tolv kanter.
Den sidoyta, som är botten kallas basyta. Även den sidoyta, som ligger överst kallas basyta. Avståndet mellan basytorna kallas rätblockets höjd.


Volymen av ett rätblock får man genom:
V = A • h Där A är basytans area och h är höjden
Kub
- En kub är ett rätblock med alla kanter lika långa.
- I en kub är alla sidoytor kvadrater.
- De sex kvadraterna är alla lika stora.


Rymddiagonalen är en sträcka, som går mellan två hörn.
Sträckan får ej ligga i en och samma sidoyta.
Volymen av en kub får man genom:
V = a • a • a Där a är kubens sida
Prisma
En prisma har två likadana månghörningar som basytor.
Sidoytorna är rektanglar.
I ett rakt prisma är sidoytorna vinkelräta mot basytorna.




Volymen av en prisma: V = A • h där A = basytans area och h = prismats höjd.
Cylinder



r = radie (d = 2•r)
h = höjd
Volymen = B•h = π•r•r•h
Mantelytan (cylinderns buktiga yta) = π•d•h
Totala begränsningsytan = π•d•h + 2•π•r•r
4. Begränsningsyta och mantelarea – Geometri
Om vi summerar alla areor från alla ytor eller sidor på en kropp, får vi den så kallade begränsningsytan. Den välvda ytan på cylindern (eller t.ex. en kon) kallas för mantelarea.
Exempel 1:



Mantelytan (cylinderns buktiga yta) = π•π•h
Totala begränsningsytan = π•d•h + 2•π•r•r
5. Klot och kon
Klot
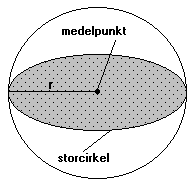

Ett klot, även kallad sfär, begränsas av en buktig yta, klotytan.
Klotets radie (r) är avståndet från klotytan till klotets medelpunkt.




Kon
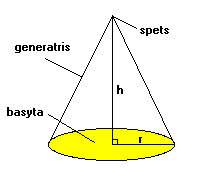

En kon begränsas av en cirkelformad basyta samt en buktig yta, mantelytan.
Generatrisen är en linje, som går från spetsen till basytans periferi.
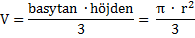
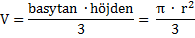
6. Vinklar






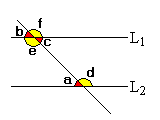

a och b är likbelägna vinklar
b och c är vertikalvinklar
a och c är alternatvinklar
b och f är sidovinklar


En fulländad cirkel är 360°. Ett varv är detsamma som 360° och ett halvt varv däremot är detsamma som en halv cirkel och följaktligen 180°.
7. Vinkelsumma
Vinkelsumman innebär summan av alla vinklar i en figur. Nedan ser du några exempel.
Exempel 1:


Vinkelsumman i en triangel är alltid 180°
ΛA + ΛB + ΛC = 180°Där Λ betyder vinkel
Exempel 2:
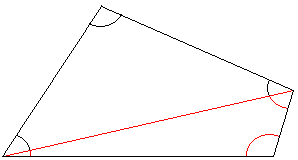
Med hjälp av en diagonal kan en fyrhörning delas upp i två trianglar.
Summan av vinklarna blir därför:
2∙180° = 360°

8. Trianglar
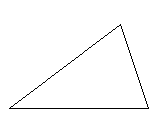

Spetsvinklig triangel, alla vinklar mindre än 90°
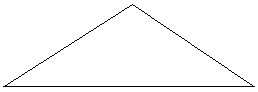

Trubbvinklig triangel, en vinkel större än 90° men mindre än 180°
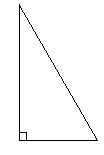

Rätvinklig triangel, en vinkel är 90°


Liksidig triangel. Alla vinklar är lika stora, dvs 60°, och alla sidor lika långa.


Likbent triangel, sidorna a är lika långa, ΛA och ΛB lika stora
9. Skala
Om en byggnadsingenjör vill göra en ritning av ett hus, kan han inte göra det i naturlig storlek. Han måste göra en förminskning av verkligheten. På samma sätt gör en kartritare naturligtvis en förminskning av det landskap han kartlägger. Bilden i ett mikroskop är däremot en förstoring av verkligheten.
För att från en bild kunna veta hur långt ett mått eller ett avstånd är i verkligheten, måste man veta i vilken skala ritningen är gjord.
Skalan kan uttryckas på flera olika sätt. Vanligast är följande:


Förminskning eller förstoring
Om ettan står först betyder det att vi har en förminskning. Bilden är då mindre än föremålet eller verkligheten. Om skalan är 1:100 är en sträcka på bilden en hundradel av motsvarande sträcka i verkligheten. Om skalan är 1:10 000 är en sträcka i verkligheten tiotusen gånger större än motsvarande sträcka på bilden.
Om ettan står sist, betyder det att vi har en förstoring. Bilden är då större än föremålet eller verkligheten. Om skalan är 100:1 är en sträcka på bilden hundra gånger så stor som motsvarande sträcka i verkligheten. Om skalan är 5 000:1 är en sträcka i verkligheten bara en femtusendel av motsvarande sträcka på bilden.
En användbar formel
Om man dividerar ett avstånd på bilden, b med motsvarande avstånd i verkligheten, f får man skalan, s. Detta kan skrivas i en formel:
Skalan = bilden/föremålets = b/f
Hur stort är avståndet i verkligheten?
På en karta i skala 1:500 000 är avståndet mellan två orter 8 cm. Hur stort är avståndet i verkligheten?
Du kan tänka så här: Varje avstånd i verkligheten är 500 000 gånger så stort som samma avstånd på kartan. Du ska alltså multiplicera 8 cm med 500 000. Sedan gäller det att hålla rätt på enheterna.
Lösning 1:
Avståndet i verkligheten är 500 000 ∙ 8 cm = 4 000 000 cm = 40 000 m = 4 mil
Lösning 2:
s = b/f
1/500 000 = 8/f
f = 500 000 ∙ 8 = 4 000 000cm = 4 mil
10. Proportionering
Man använder även skalning för att ange proportioner inom geometri. TV-skärmar har ofta skalan 16:9. Detta betyder att proportionen mellan bas och höjd är 16:9. Förenklat kan vi säga att om basen är 16 cm så är höjden 9 cm. Om vi mäter att basen är 70 cm lång så kan vi helt enkelt använda proportions-skalan 16:9 för att räkna ut hur stor höjden blir. Om basen är 70 cm vet vi att den är 16/9 av höjden.
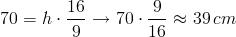
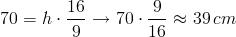
11. Likformiga trianglar
Två figurer är likformiga inom geometri om de har exakt samma form. Den ena figuren kan vara större eller mindre än den andra. Exempel på likformighet är två kartor över samma område, men ritade i olika skalor.
Exempel 1:
Triangeln ABC är en avbildning av triangeln DEF.


Alla sidor i triangeln ABC har förstorats fyra gånger. Detta medför, att de båda trianglarna är likformiga, som man säger inom geometri. De båda trianglarna har samma form men den ena triangeln är större än den andra. Motsvarande vinklar i de båda trianglarna är lika stora.
∆DEF ~ ∆ABC vilket utläses “triangeln DEF är likformig med triangeln ABC”.
~ betyder likformig med.
Om två vinklar i en triangel är lika med motsvarande vinklar i en annan triangel, måste även den tredje vinkeln vara lika stor i de båda trianglarna. Härav följer att trianglarna är likformiga.
För likformiga trianglar gäller:
- Förhållandet (kvoterna) mellan motsvarande sidor är lika stora.
- Motsvarande vinklar är lika stora.
12. Pythagoras sats
Pythagoras sats inom geometri innebär att i en rätvinklig triangel så är summan av kateternas kvadrater lika med hypotenusans kvadrat. Uttryckt i variabler innebär det detta:
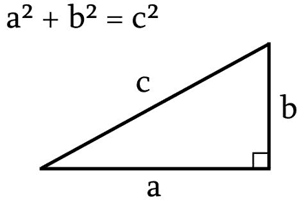

där a och b är katetlängderna och c hypotenusans längd.
Detta är sant i alla rätvinkliga trianglar.
Omvänt är alla trianglar som uppfyller Pythagoras sats rätvinkliga.
Exempel 1:
I en rätvinklig triangel är de två kateterna 3 cm och 4 cm långa. Beräkna hypotenusans längd.
Lösning:
Med a=3 och b=4 får vi med hjälp av Pythagoras sats:


Exempel 2:
I en rätvinklig triangel är en katet 5 cm lång. Den andra är x cm lång. Hypotenusan är 25-x cm lång. Bestäm x.
Lösning:
Med a=5, b=x och c=25-x får vi med hjälp av Pythagoras sats:


Svaret är alltså x=12 och kateterna är 5 cm och 12 cm långa. Hypotenusan är 13 cm lång.

