Procenträkning är viktigt i studierna såväl som vardagen. Många av de begrepp vi senare går igenom bygger på procenträkning. Procenträkning har också en viktig roll i privatekonomin, exempelvis vid ränteberäkningar. Därför är vi jätteglada att du väljer använda vår sammanfattning för att förbättra dina kunskaper inom procenträkning.
Läs vidare om procenträkning även under avsnittet om Statistik
Överblick:
1. Procenten, delen och det hel
2. Tre grundläggande problem
3. Förändringar i procent
4. Procentenheter
5. Större än det hela
6. Förändringsfaktor
7. Upprepade procentuella förändringar
1. Procenten, delen och det hela
Ett annat namn för procent är hundradelar, exempelvis är 50% lika med 50 hundradelar.
Vi kan alltså uttrycka andelen på flera olika sätt:



2. Tre grundläggande problem med procenträkning
En mycket viktig sak att kunna vid räkning med procent är att kunna omvandla ett värde i bråkform till procentform. Det första som måste göras är att omvandla bråket till decimalform. Sedan multiplicerar du talet i decimalform med hundra för att få ut procentsatsen. Se nedan.



Det andra grundläggande problemet du måste behärska är att kunna beräkna andelen om du har det hela och procentsatsen. Med andra ord ska du exempelvis kunna beräkna vad 25% är av 200. För att räkna ut detta ska du utnyttja att 25% = 0.25 för att sedan multiplicera 0.25 med 200.
25% × 200 = 0.25 × 200 = 50
Det sista problemet är när vi söker det hela. Då har vi procentsatsen och delen, och eftersom procent är hundradelar kan vi lätt räkna ut vad en hundradel är genom att dela delen med antalet procent. Sen är det enkelt att multiplicera med hundra för att få det hela:


En procent är alltså 4.


3. Förändringar i procent
Om ett pris på en tröja ändras kan det ibland vara bra att veta hur stor denna förändring är i procent. Om vi vet det gamla respektive det nya priset kan vi räkna ut denna förändring.
Exempel 1:
Låt oss säga att denna tröja från början kostade 500 kr. Sedan höjs priset till 600 kronor, med hur många procent har priset ökat?
- Beräkna först förändringen dvs 600-500 = 100
- Sedan dividerar du förändringen med det ursprungliga priset, det vill säga;
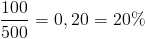
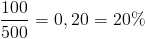
Hade värdet istället minskat, så hade vi delat minskningen med det gamla värdet.
Exempel 2:
Antag att du får 20 % rabatt på en vara som från början kostade 300 kr. För att då räkna ut det nya priset räknar du först ut vad 20 % är av 300 kr, dvs. 0.20 × 300 = 60. Nu vet vi alltså att 20% av 300 kr är 60kr.
Svar: Det nya priset blir då 300 – 60 = 240
Exempel 3:
Antag att Peter har kvar 75 kr efter att ha betalat en avgift på 2,75 % av inköpspriset. Vad är inköpspriset?
- X kr = Beloppet före avgiften (inköpspriset).
- (X x 0,0275) = avgiften, dvs. 2,75% av beloppet X.
- 75 kr = beloppet efter att avgiften på 2,75% är betald.
Sätt in ovan premisser i en funktion:
X – (X x 0,0275) = 75
Funktionen säger “av beloppet X, subtraheras en avgift på 2,75% av beloppet X, detta resulterar i 75 kr kvar av beloppet X”. Så låt oss nu räkna ut vad beloppet X är:
X – 0,0275X = 75
0,9725X = 75
X = 77,120822…
Svar = Beloppet X innan en avgift på 2,75% är 77,12 kr.
4. Procentenheter
Det är mycket viktigt att skilja på procent och procentenheter. Detta beskrivs med ett exempel:
Exempel 1:
Rabatten på en vara sänktes från 25% till 20%. Varan har då sänkts med 5 procentenheter (25-20=5) och sänkts med 20 procent (5/25 = 0.20 = 20%). Om du inte förstår det sistnämnda, ta då en titt på föregående avsnitt ”3. Förändringar i procent”.
5. Större än det hela
100% är det vi kallar ”det hela”, det vill säga allting. Kan något öka med mer än 100%? Ja, det kan det faktiskt. Antag att en bil kostar 30 000kr och att priset ökar till 90 000 kr, då har bilens värde ökat med 200%, eftersom 60 000/30 000 = 2 = 200% (60 000 = prisökningen, dvs 90 000-30 000 kr).
6. Förändringsfaktor i procenträkning
När det gäller beräkningar av procentuell förändring så kan det underlätta att använda en s.k. förändringsfaktor (även kallad ändringsfaktor eller ibland tillväxtfaktor).
En förändringsfaktor är, precis som namnet anger, en faktor som ett ursprungsvärde ska multipliceras med för att få ett slutvärde.
Förändringsfaktorn bestäms genom att utgå från 100% (ursprungsvärdet) och sedan addera (om det är en ökning) eller subtrahera (om det är en minskning) procenttalet.
Exempel 1:
27 % ökning innebär 100 % + 27 % = 127 % = 1,27
Dvs. förändringsfaktorn är 1,27
27 % minskning innebär 100 % – 27 % = 73 % = 0,73
Dvs. förändringsfaktorn är 0,73
Förändringsfaktorn kan användas på följande sätt:
Förändringsfaktorn × Ursprungsvärdet = Slutvärdet
För att visa detta mer konkret så följer här samma exempel som i föregående avsnitt. Denna gång används förändringsfaktorer i beräkningarna.


Exempel 2:
Huspriserna i ett område ökar på grund av större efterfrågan. Ägarna till ett hus som köptes för 750 000 kronor hoppas få 20 % mer vid försäljning. Vilket pris hoppas de på?
20 % ökning motsvarar förändringsfaktorn 1,2
(eftersom 100 % + 20 % = 120 % = 1,20 = 1,2).
Säljarna hoppas följaktligen få 1.2 × 750 000 = 900 000 kronor.
Exempel 3:
På grund av utfiskning minskade en fiskares årliga fångst med 32 %. Hur stor var fångsten efter minskningen om den året innan var 200 ton?
32 % minskning motsvarar förändringsfaktorn 0,68
(eftersom 100 % – 32 % = 68 % = 0,68).
Alltså var fångsten 0.68 × 200 = 136 ton.
7. Upprepade procentuella förändringar
Förändringsfaktorn är även användbar när flera procentuella förändringar sker efter varandra. En stor fördel är att något ursprungsvärde inte behövs när den totala procentuella förändringen ska bestämmas.
Exempel 1:
Råvarupriset för en sällsynt typ av ädelsten förändrades på följande sätt under fyra år:
Första året: en ökning med 12 procent, +12 %
Andra året en minskning med 7 procent, –7 %
Tredje året en minskning med 3 procent, –3 %
Fjärde året en ökning med 8 procent, +8%
Ökade eller minskade priset totalt sett under dessa fyra år? Med hur många procent?
+12 % motsvarar förändringsfaktorn 1,12
(eftersom 100 % + 12 % = 112 % = 1,12)
–7 % motsvarar förändringsfaktorn 0,93
(eftersom 100 % – 7 % = 93 % = 0,93)
–3 % motsvarar förändringsfaktorn 0,97
(eftersom 100 % – 3 % = 97 % = 0,97)
+8 % motsvarar förändringsfaktorn 1,08
(eftersom 100 % + 8 % = 108 % = 1,08)
Den totala förändringsfaktorn är 1.12 × 0.93 × 0.97 × 1.08 = ca 1,09
Förändringsfaktorn 1,09 motsvarar 9 % ökning (eftersom 1,09 = 109 % = 100 % + 9 %)
Totalt har priset för ädelstenen ökat med 9 % under de fyra åren.
Exempel 2:
Ett annat sätt att beräkna upprepade förändringar är när upprepningen är en procentuell konstant förändring över en period. Låt oss säga att Lisa placerar 2 000 kr i en fond som ger en konstant avkastning på 10% per år, vad är pengarna värda om 3 år?
Detta går att beräkna enligt exempel 1 med en förändring med 1,10 för varje år. Men ett annat sätt att räkna det på är enligt följande formel:
y = d (1+r)^p. Här är “y” framtidens värde av ett belopp idag “d”. “r” utgör den konstanta räntan och “p” beskriver periodens länd. Låt oss räkna ut frågan:
y = d (1+r)^p
y = 2 000 (1+ 0,10)^p
y = 2 000 x (1,1)^p
y = 2 000 x (1,1)^år
y = 2000 x (1,1)^3
y = 2000 x 1,331 = 2 662 kr
Svar: Med en konstant, procentuell förändring av + 10% per år, är beloppet 2 000 kr efter 3 år värt 2 662 kr.

