Funktioner kan beskriva alltifrån hur priset på godispåsen varierar med hektopriset för godis till avancerade processer i miljön, industrin eller kroppen. Vi bekantar oss med funktioner i avsnittet, det är faktiskt rätt skoj!
Innehåll – Funktioner:
1. Koordinatsystem
2. Grafer
3. Linjära funktioner
4. Positiva potenser
5. Negativa potenser
6. Grundpotensform
7. Prefix
8. Enhetsanalys
9. Exponentialfunktioner
10. Potensekvationer
1. Koordinatsystem
Funktioner beskriver samband. Här nöjer vi oss med att endast studera samband mellan två storheter. Det kan exempelvis gälla sambandet mellan hur långt en bil färdats och hur lång tid färden pågått. Det kan även gälla hur många samtalsminuter någon har för sin mobiltelefon under en månad och hur stor räkningen blir (dvs. hur stor kostnaden är) för denna månad.
Funktioner kan beskrivas på flera sätt. Ett sådant sätt är att använda en graf (kallas även funktionsgraf) ritad i ett koordinatsystem.
Ett koordinatsystem består av två mot varandra vinkelräta talaxlar, s.k. koordinataxlar. Dessa skär varandra i sina nollpunkter. Denna skärningspunkt kallas origo. Den horisontella koordinataxeln kallas x-axeln (kallas även första axeln) och ritas i regel åt höger. Den vertikala axeln kallas y-axeln (kallas även andra axeln) och ritas i regel uppåt.
Här följer ett exempel på hur ett koordinatsystem kan se ut:


I ett koordinatsystem kan punkter markeras. I nedanstående exempel har tre punkter markerats:
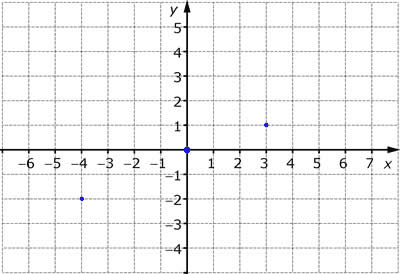

För att kunna referera till en punkt i ett koordinatsystem används punktens x-koordinat (kallas även första koordinat) och y-koordinat (kallas även andra koordinat). Dessa bestäms genom att förflytta sig från punkten i höjdled till x-axeln och i sidled till y-axeln. Koordinaterna skrivs med x-koordinaten först och y-koordinaten sedan. De är omgivna av parenteser och separerade av ett semikolon eller ett komma. Ovanstående tre punkter kan skrivas på följande sätt:


2. Grafer
En graf utgörs ofta av en kurva eller linje. En viktig matematisk förmåga är att kunna avläsa och tolka grafer och funktioner .


Exempel 1:
En djurforskare har kopplat en liten sändare på en ödla för att se hur långt den förflyttar sig från sitt bo.
Nedanstående graf visar avståndet mellan ödlan och boet under en 13-minutersperiod.


Ur grafen kan vi exempelvis hämta information för att besvara frågan:
”Hur långt från boet befinner sig ödlan efter sju minuter?”
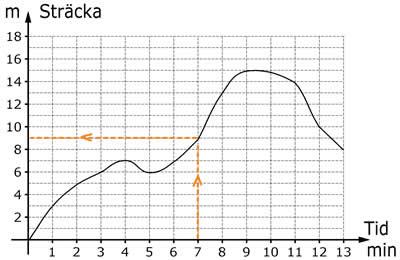

Genom att utgå från tidpunkten ”7 minuter” på x-axeln, sedan förflytta sig rakt upp till grafen och därefter åt sidan till y-axeln, kan sträckan ”9 meter” avläsas.
Dvs. ödlan befinner sig nio meter från boet efter sju minuter.
Observera att med ”efter sju minuter” menas ”vid tidpunkten sju minuter”.
En annan frågeställning som kan besvaras med hjälp av diagrammet är:
”När befinner sig ödlan sex meter från sitt bo?”
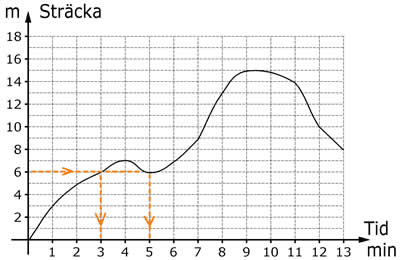

Genom att utgå från sträckan ”6 meter” på y-axeln, sedan förflytta sig rakt åt sidan till grafen och därefter ned till x-axeln, kan tiden ”3 minuter” avläsas. Dessutom finns det ytterligare en tidpunkt som motsvarar sträckan ”6 meter”, nämligen ”5 minuter”.
Frågan har alltså två svar:
Ödlan befinner sig sex meter från boet vid två tidpunkter, efter tre minuter och efter fem minuter.
3. Linjära funktioner
En funktion vars graf är en rät linje är en linjär funktion.
Formeln hos en linjär funktion har alltid följande principiella utseende:
y = kx + m
k och mär konstanter, dvs. tal. Observera att de kan vara noll. k kallas riktningskoefficient och påverkar linjens lutning. m är den y-koordinat där linjen skär y-axeln.
Exempel 1:
y = 3x + 1
En värdetabell konstrueras genom att välja några godtyckliga x-värden och sedan räkna ut respektive y-värde. Varje sådant par av x- och y-värden är koordinaterna för en punkt på grafen. Punkterna ritas in och sammanbinds med en rät linje (eftersom det är en linjär funktion).




Exempel 2:
y = x – 4
En värdetabell konstrueras genom att välja några godtyckliga x-värden och sedan räkna ut respektive y-värde. Varje sådant par av x- och y-värden är koordinaterna för en punkt på grafen. Punkterna ritas in och sammanbinds med en rät linje (eftersom det är en linjär funktion).


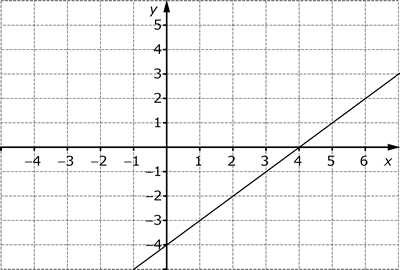

Exempel 3:
y = 5 – 2x
En värdetabell konstrueras genom att välja några godtyckliga x-värden och sedan räkna ut respektive y-värde. Varje sådant par av x- och y-värden är koordinaterna för en punkt på grafen. Punkterna ritas in och sammanbinds med en rät linje (eftersom det är en linjär funktion).




Exempel 4:
y = 4
Detta är en linjär funktion eftersom y = 0 ∙ x + 4.
Här behövs ingen värdetabell eftersom y-värdet är oberoende av x. För alla punkter på grafen gäller att y = 4, dvs den utgörs av en horisontell rät linje som skär y-axeln där y = 4.


4. Positiva potenser
Istället för att repetera och skriva samma matematiska operation flera gånger, så finns det genvägar. På sätt och vis är multiplikation en genväg för att slippa skriva 2+2+2+2. Istället skriver vi ju 2 ∙ 4.
Det finns en liknande genväg vad gäller multiplikation:
2∙2∙2∙2 = 16(Faktorform)
24 = 16(Potensform)
Uttrycket läses “2 upphöjt till 4” och kallas potens. 2:an kallas för bas och 4:an kallas för exponent:
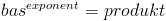
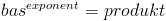
Vad gäller multiplikation och division med potenser, så finns det färdiga formler:




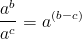
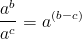
Annars måste vi göra om räkna ut potenserna och räkna ut talen.
5. Negativa potenser
Det spelar inte någon roll om det förekommer negativa exponenter, räknereglerna är desamma:


Men vad är ![]()
![]()
Om vi räknar lite baklänges och samtidigt kommer på två termer (2 och 7) vars differens blir -5 så får vi följande samband:


Formeln lyder alltså:


Detta gäller även omvänt:


Om något är upphöjt till noll, och vi vill beräkna detta kan vi utnyttja de hittills angivna räknereglerna att ta reda på vad det blir. Vi vet att:
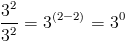
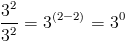
Samtidigt vet vi att:
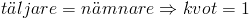
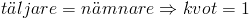
Det vill säga att:
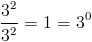
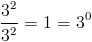
Regeln som gäller är alltså alltid, oavsett vad “a” är:


6.Grundpotensform
Grundpotensform är ett kompakt sätt att skriva tal som heltalsexponenter med 10 som bas. Formen används framför allt för att skriva tal som är mycket stora eller mycket små.
101 = 10
102 = 100
103 = 1 000
106 = 1 000 000
109 = 1 000 000 000
1020 = 100 000 000 000 000 000 000
10-1 = 1/10 = 0,1
10-3 = 1/1 000 = 0,001
10-9 = 1/1 000 000 000 = 0,000000001
Genom att använda grundpotensform kan ett stort tal som 156 234 000 000 000 000 000 000 000 000 lättare skrivas som 1,56234∙1029, och ett litet tal som 0,0000000000234 kan skrivas som 2,34∙10-11.
Ett tal skrivet i grundpotensform kan delas upp i två delar, först siffervärdet, därefter tiopotensen. För att talet ska vara skrivet i grundpotensform krävs att siffervärdet är ett tal som är större än eller lika med 1 och mindre än 10.
De flesta kalkylatorer (miniräknare) och vissa datorprogram utelämnar bas-siffran 10 och använder bokstaven E (som i Exponent) istället, till exempel 1,56234 E29. Detta E ska inte förväxlas med talet e. Det finns även datorprogram (till exempel programmeringsspråket QBasic) som använder bokstaven D istället då man anger tal på dubbelprecisionsformat.
7. Prefix
För att slippa skriva väldigt stora mätetal och kunna minska antalet olika enheter använder man sig av sk prefix för att ange multiplar (hur många) av grundenheterna. Prefixen anges med en bokstav. Bokstaven k betyder 1000, dvs 1 km betyder 1000 m, kg betyder 1000 g, kW betyder 1000 W och så vidare. Som du ser använder du dig redan av en del prefix. Du bör kunna följande prefix utan att titta i någon bok eller formelsamling.


8. Enhetsanalys
Enhetssanalys är något väldigt användbart när det kommer till att räkna och hålla ordning på enheter samtidigt. På samma sätt som vi räknar in enheten så kan vi räkna med endast enheter – det har vi ju sett med cm2 och cm3. Exempel: En bil kör 80 km på 2 timmar. Vilken var medelhastigheten?
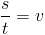
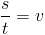


För att försäkra oss om att enheten i svaret verkligen blir km/h så kan vi räkna endast med enheter och prefix:
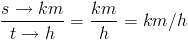
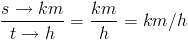
Denna typ av analys kan även användas för att reda ut om de enheter man får i uppgiften inte är SI. Exempel: En bil kör 9 mil på 60 minuter. Vilken var medelhastigheten? I detta exempel kan vi inte bara sätta in 9 och 60 direkt i formeln och förvänta oss att enheten blir km/h. Antingen kan vi sätta in 9 och 60 i formeln och se vad den resulterande enheten blir och sedan eventuellt göra om svaret till SI-enheter:


eller också så kan man göra om enheterna direkt, så att man tydligt ser att svaret kommer att bli rätt:


9. Exponentialfunktioner
När en procentuell förändring över tid ska studeras, är det ofta användbart att använda förändringsfaktorn.
Exempel 1:


En tillverkare av etanolbilar räknar med att öka sin försäljning av bilar med 12 % per år. Förra året sålde de 9 000 bilar.
12 % ökning motsvarar förändringsfaktorn 1,12 (eftersom 100 % + 12 % = 112 % = 1,12).
Efter 1 år bör försäljningen vara
9 000 ∙ 1,12 = 10 080 bilar
Efter 2 år bör försäljningen vara
9 000 · 1,12 · 1,12 = 9 000 · 1,122 ≈ 11 290 bilar
Efter 3 år bör försäljningen vara
9 000 · 1,12 · 1,12 · 1,12 = 9 000 · 1,123 ≈ 12 644 bilar
Efter 3 år bör försäljningen vara
9 000 · 1,12 · 1,12 · 1,12 · 1,12 = 9 000 · 1,124 ≈ 14 162 bilar
Här framträder ett mönster:
Efter 1 år bör antalet sålda bilar vara 9 000 · 1,121
Efter 2 år bör antalet sålda bilar vara 9 000 · 1,122
Efter 3 år bör antalet sålda bilar vara 9 000 · 1,123
Efter 4 år bör antalet sålda bilar vara 9 000 · 1,124
…
Efter x år bör antalet sålda bilar vara 9 000 · 1,12x
Detta kan skrivas som en funktionsformel: y = 9 000 · 1,12x , där y är antalet sålda bilar efter x år.
Eftersom den oberoende variabeln är en exponent så kallas denna typ av funktion för exponentialfunktion.
Allmänt kan en exponentialfunktion skrivas:
y = C·axdär C = startvärdet
och a = förändringsfaktorn
Exponentialfunktioner används alltså i regel för att beskriva procentuella förändringar.
Formeln är användbar oavsett om det handlar om en procentuell ökning eller minskning.
Exempel 2:


Ett forskarteam bevakar ett havsområde eftersom delfinerna av okänd anledning överger området. Från början finns det 850 delfiner i området och forskarna märker att antalet delfiner minskar med 10 % per månad.
En minskning med 10 % motsvarar förändringsfaktorn 0,9 (eftersom 100 % – 10 % = 90 % = 0,9)
Förändringen av antalet delfiner kan beskrivas med exponentialfunktionen
y = 850 · 0,9x , där y är antalet delfiner efter x månader.
10. Potensekvationer – Funktioner
Nedan finns alla potensregler du behöver kunna i Matematik 1.



