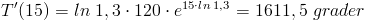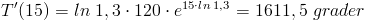Här fortsätter vi förra delens arbete med logaritmer. Vi fokuserar på en speciallogaritm som kallas naturliga logaritmer
Innehåll – Naturliga logaritmer:
1. Talet “e“
2. Härledning av f'(x) = ex
3. Nyttan av e
1. Talet “e“
Talet e är benämningen vi har på det tal som man tar upphöjt med x för att få en kurva vars tangent i punkten (0,1) har riktningskoefficienten 1.
Om vi kikar på dessa tre nedanstående kurvor, så ser vi i första bilden att tangenten till kurvan:
y = 2x i punkten (0,1) får en riktningskoefficient på ungefär 0,7.


I andra bilden ser vi att riktningskoefficienten för tangenten till kurvan y=4x i punkten (0,1) blir ca 1,4.


I tredje bilden försöker vi hitta det tal som upphöjt till x blir en kurva vars tangent får riktningskoefficienten 1 i punkten (0,1). Detta tal måste enligt föregående bilder ligga någonstans mellan 2 och 4.
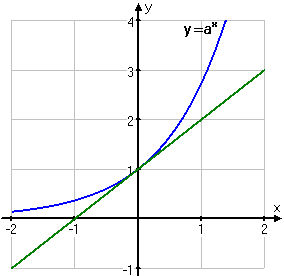

Efter vissa uträkningar, som jag inte har för avsikt att ta upp, så kommer man fram till att talet blir 2,718 28…osv, det är alltså detta tal som har betecknats med e.
Tangenten till kurvan y = ex i punkten (0,1) har alltså riktningskoefficienten 1. Det innebär även att om vi sätter att f(x) = ex så blir derivatan av det: f'(0 )= 1.
f'(x) = ex → f'(0) = e0 = 1
2. Härledning av f'(x) = ex
Innan vi ska gå vidare och visa meningen och nyttan med detta “magiska” tal ska vi först härleda och visa att derivatan av f(x) = ex faktiskt är f'(x) = ex.
Vi börjar med derivatans h-definition, som vi gått igenom i tidigare kapitel:


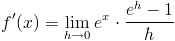
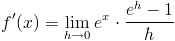
Nu kan vi inte beräkna mer, utan vi får själva testa vad som händer om h går mot noll:


Vi ser att uttrycket går mot 1, och kvar blir bara ex!
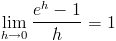
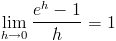


Alltså:
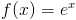
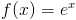
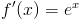
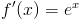
Vi ska titta på en till härledning innan vi går vidare. Vi ska derivera:
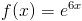
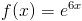
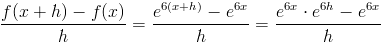
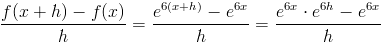




Om vi nu åter igen sätter in ett tal som är väldigt nära noll, till exempel 0,0000001 blir derivatan:




Den allmänna formeln, där k är en konstant, lyder:
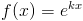
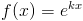



3. Nyttan av e
Vad har vi nu för nytta av e? Varför är det så intressant att talet 2,718x har en derivata som är densamma? Kommer du ihåg att vi sa att ett tal kan skrivas om till 10-potensform. Vilket positivt tal som helst kan skrivas om som 10en siffra
Till exempel är:


Men faktum är att 3 även kan skrivas om som:


Man kan skriva om 3 till VilketTalSomHelstEnSiffra
Alla exponentialfunktioner kan ritas som kurvor och på så sätt hjälpa oss med dessa omskrivningar:
Denna figur visar kurvorna för 5 olika exponentialfunktioner:
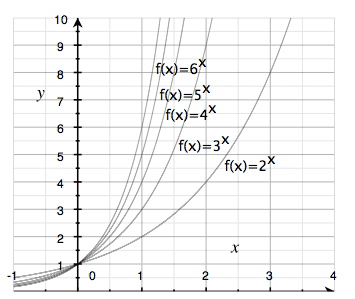

Här kan vi se och bekräfta det vi skrev ovanför, att till exempel så är:
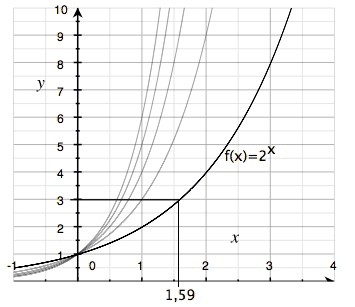

Om vi kan skriva om 3 till VilketTalSomHelstEnSiffra så kan vi alltså även skriva om 3 som:
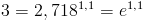
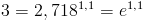
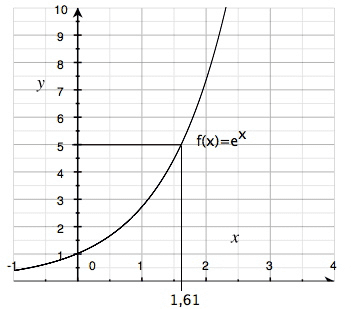
I följande figur är kurvan till f(x) = ex inritad:


Genom att ha denna graf till hands så kan vi läsa ut och lösa alla ekvationer som innehåller y = ex. Till exempel:



Alltså:


Även denna “uppritning och avläsning” kan miniräknare göra automatiskt åt oss. Funktionen betecknas “ln”:
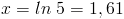
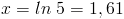
Denna funktion fungerar alltså precis som tio-logaritmer, men kallas för naturlig logaritm.
Nu ska vi utnyttja detta skrivsätt och skriva om 5:
Jämför med 10-potensen.
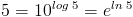
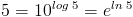
Vad har vi nu för nytta av att skriva om 5 till en naturlig logaritm? Jo! Nu har vi möjlighet att enkelt derivera en exponentialfunktion!!
Exempel 1:


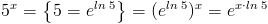
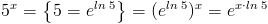


Denna funktion är nu väldigt enkel att derivera. Vi tillämpar följande regel:



och får:
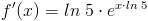
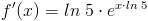
Vi har alltså bara skrivit om uttrycket, eller 5an rättare sagt, och formulerat ett uttryck som vi vet hur man deriverar.
(Varje gång vi ser “konstiga” formler som innehåller ett “e” så är detta i själva verket ett redan omskrivet uttryck – vi kan se det som att någon redan gjort oss en tjänst och skrivit ut ett uttryck och förenklat åt oss. Någon har redan “ritat upp och läst av grafen” och fått ut ett värde baserat på talet e. Från början fanns det ett exponentiellt uttryck med x i exponenten.)
För att ha god användning av talet e och utnyttja detta vid derivering, är det viktigt att vi först och främst vet hur vi skriver om en exponentialfunktion. Formen som vi vill ha är y = ekx.


Exempel 2:
Temperaturen (T) i en ugn ökar enligt följande funktion, där x är tiden i minuter. Beräkna temperaturökningen vid tiden 15 minuter:


Lösning: