Man illustrerar elektriska fält som linjer. Ju tätare linjerna ligger desto starkare blir fältet. Fältriktningen bestäms av hur kraften på en positivt laddad testpartikel är riktad.
Elektrisk fältstyrka
Detta är en storhet som ofta används vid elektriska fält och räknas ut på detta vis:
E=F/q där F är kraften som en partikel påverkas av i fältet och q är partikelns laddning.
Alltså:
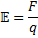
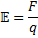
Coulombs lag
Två laddningar påverkar alltid varandra. Med hjälp av Coulombs lag kan man räkna ut med vilken kraft dessa två laddningar påverkar varandra.
där q och Q är de bägge laddningarnas storlekar, r är avståndet mellan laddningarna och k är en konstant på ca 8,99×109.
Sammanslagning av ovanstående regler
Ibland är det intressant att veta fältstyrkan mellan två laddningar när de har ett visst avstånd mellan sig. Vi vill gärna visa hur man kan kombinera de två formlerna vi lärt oss med ett exempel.
Exempel:
Bestäm den elektriska fältstyrkan i en punkt 3,0 cm från en punktformig laddning(Q) på 25 fC.
Lösning:
Det första att tänka på är att laddningarna påverkar varandra med precis lika stora krafter. De formler vi lärt oss gäller därför för bägge laddningar.
ger att
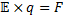
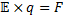
Vi vet även att
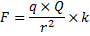
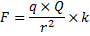
Om vi sedan skriver ihop formlerna får vi följande:
Detta kan förenklas till att:
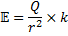
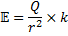
Nu råkar vi veta att Q = 25fC = 25×10-15C och avståndet(r) är 3,0 cm.
Alltså är den elektriska fältstyrkan ungefär 0,25N/C
Spänning
Nu tänker vi oss precis som i bilden att en positivt laddad platta och en negativt laddad platta ger upphov till en spänning(U). En liten negativ laddning placeras nu mellan de bägge plattorna, alltså i det elektriska fältet.
Om vi bortser från gravitationen(vilket vi kan) så kommer den negativa laddningen att ”falla” mot den positiva plattan. Under fallet omsätts energin E. Nu ska vi se vad vi kan dra för slutsats utifrån detta.
Vi börjar med att inse att den fallande laddningen utför ett arbete när den faller som kan beskrivas med formeln:
(gammal kunskap förhoppningsvis). Skillnaden mellan arbete och energi är väldigt diffus och därför kan vi säga att lägesenergin som laddningen förlorar under fallet, det vill säga energin som omsätts, kan beskrivas på följande vis:
(d är precis som s en beteckning för sträckan som vi använder i figuren)
Om vi även kommer ihåg från förra exemplet att 
så kan följande konstateras:
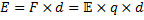
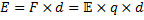
Sedan tidigare vet vi även att 
Nu slår vi ihop dessa två formler och säger att:
Genom att q tar ut varandra och en enkel omskrivning får vi att:
Enheten blir här V/m
En intressant slutsats kan dras av detta: Den elektriska fältstyrkan i en viss punkt är lika stor oavsett hur stor laddning som är i fältet.
Notera även att elektrisk fältstyrka kan ha två enheter: N/C och V/m. Du kan använda vilken du vill men det snyggaste är väl att använda enhet utefter vilken formel du har använt.
OBS! Formeln och alla konstateranden gäller bara i homogena fält.
Hur hög fart har elektronen när den lämnar det elektriska fältet?
Detta är en klassisk uppgift som med rätt metoder är relativt lätt och kan generera många härliga poäng så se till att förstå det här.
I exemplet nedan har vi en elektron som faller från den negativa plattan i ett elektriskt fält och flyger ut ur den positiva plattan genom ett litet hål. Uppgiften är att räkna ut vilken hastighet elektronen har precis när den lämnar hålet och inte påverkas av fältet något mer.
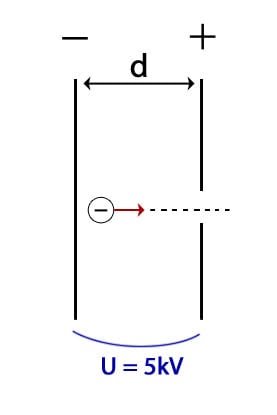
Lösning
Vi vet att spänningen(U) är 5000V och att laddningen på elektronen är 1,602×10-19C(elementarpartikelns laddning). Dessutom vet vi att elektronens massa är 9,11×10-31kg.
Lägesenergin som elektronen har från början är 
. All denna energi omvandlas till rörelseenergi:
Om Ek = E så är:
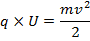
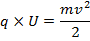
Nu bryter vi ut (v) ur denna formel:
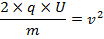
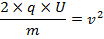
Nu sätter vi in våra värden:
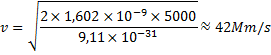
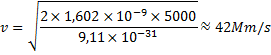
Svar: Elektronen har hastigheten 42Mm/s!
Elektriskt fält i ledare
I en ledare är det elektriska fältet riktat i samma riktning som ledaren. Det är homogent och kan beskrivas med samma formel som elektriskt fält mellan två plattor, det vill säga:
Observera att l som i detta fall motsvarar längden är ekvivalent med d i tidigare formel.
Potential
Detta är en antagligen en ny term för de flesta av er. Det är en storhet som betecknas V. Egentligen är spänningen en potentialskillnad mellan två punkter och potentialen är ungefär spänningen i en punkt. Detta kommer att beskrivas närmare nedan. För att göra detta måste vi bestämma ett nolläge där vi säger att potentialen är noll. Vi ska börja med att titta på potential med avseende på punkter som ligger mellan två elektriskt laddade plattor. Sedan kommer vi att beskriva potentialen i kretsar.
Potential mellan punkter som ligger mellan två elektriska plattor
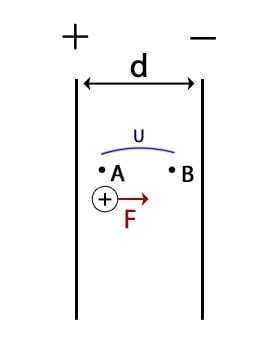
I bilden ser vi en positiv laddning som faller från punkt A till punkt B. Då kommer den att förlora lägesenergi och enligt sambandet E=q×U så måste ju U minska om E blir mindre eftersom laddningen q för partikeln är konstant. Om vi räknar på energiskillnaden (i lägesenergi) mellan de bägge punkterna så bör vi kunna se hur spänningen skiljer sig mellan de bägge punkterna.
Vi har satt den negativa plattan till potentialen 0, vi säger att den jordats.
Om energiskillnaden i lägesenergi betecknas ΔE så kan vi säga att spänningen är:
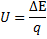
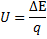
Notera att detta är en formel vi använt tidigare, bara att vi stället för ΔE lite slarvigt har skrivit E.
Nu är det så att potentialen är lite slarvigt spänningen i en punkt:
Alltså är
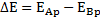
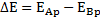
vilket är skillnaden i potentiell energi mellan punkterna A och B.
Då kan sägas att 
Potentialvandring i en sluten krets
I en krets är potentialen över strömkällan lika med spänningen under strömkällan. Om vi utgår från denna potential och vandrar ett varv runt kretsen så kommer potentialen att sjunka till noll när vi når slutet av kretsen(minuspolen). Nedan kommer ett exempel på hur man kan göra en potentialvandring:
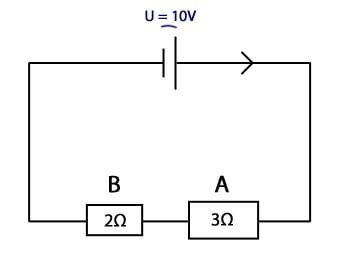
I kretsen ovan har vi spänningen 10 V över strömkällan, strömmen 2A genom kretsen och resistans A på 3Ω och resistans B på 2Ω.
Nu vandrar vi!
Från pluspolen har vi potentialen 10V. Sedan går vi över resistans A. Över denna resistor ligger spänningen 6V (U=R×i ). Efter att ha passerat denna är potentialen 10V-6V=4V. Potentialen mellan strömkällan och resistor A är alltså 6V. Över resistor B ligger spänningen 4V och när vi passerar denna kommer potentialskillnaden bli 4V mindre, alltså 0V. Nu har vi nått minuspolen och vi kan konstatera att potentialen runt en hel krets är noll.
Om vi istället vandrar mot strömmen(från minuspol till pluspol) så får säga att potentialen från början är 0V och sedan ökar den för varje resistor man vandrar över. I detta fall alltså:
Potentialen över kretsen blir alltså den samma åt vilket håll man än vandrar och den blir lika stor som spänningen över kretsen. Detta är väldigt logiskt eftersom spänningen är potentialen mellan två punkter(i detta fall pluspolen och minuspolen).
Elektronstrålerör
Ett elektronstrålerör är ett rör dit elektroner kommer in och påverkas av ett elektriskt fält. Detta elektriska fält trycker dem i olika riktningar. Detta används bland annat i gamla TV-apparater. Detta kan påvisas genom att man tar en magnet och håller den nära en gammal TV som är på. Då kommer man se hur färgerna flyttar sig för att elektronerna i elektronstråleröret påverkas av magneten. En varning med detta är att man kan ha sönder TV:n om man gör det för länge.
Nu ska vi dock åter bli allvarliga och lära oss att räkna på elektronstrålerör:
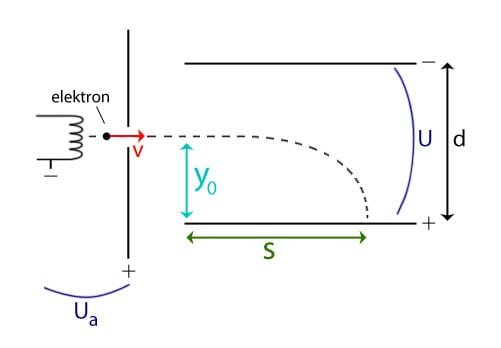
I bilden ovan har vi accelererat en elektron i ett elektriskt fält med spänningen UA och den får farten 20Mm/s. Denna elektron går sedan in i ett elektronstrålerör med ett elektriskt fält och som trycker elektronen ner i pluspolen.
Nu ska vi titta på hur stor spänningen UA är:
Om elektronens hastighet är 20Mm/s när den går in i elektronröret så har den rörelseenergin:
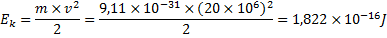
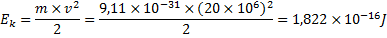
Denna energi måste vara lika med den elektriska lägesenergi som elektronen har innan den accelereras.
Alltså Ep = Q×UA, då Ep = Ek så är 1,822×10-16J = Q×UA
Då elektronens laddning Q är 1,602×10-19C så gäller:
I vårt fall har vi ingen v0y då elektronen kommer in helt vågrätt. Dessutom är y0 = 0,012m
Denna energi måste vara lika med den elektriska lägesenergi som elektronen har innan den accelereras.
Alltså 
, då Ep=Ek så är 
Då elektronens laddning Q är 1,602×10-19C så gäller:
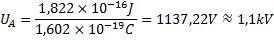
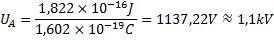
Svar: Spänningen över det accelererande elektriska fältet är 1,1kV.
Nu tittar vi på figuren igen. Vi ser att höjden som elektronen har över pluspolen när den kommer in i fältet är markerad y0, att bredden på elektronröret är markerad d och att spänningen över elektronröret är markerad som U.
Vi säger följande:
y0 = 0,012m
d = 0,02m
U = 1000V
Då kan vi räkna ut hur långt elektronen hinner i vågrätt led innan den träffar den positiva plattan, alltså sträckan S i figuren.
Så här kan detta göras:
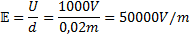
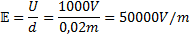
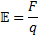
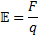
Alltså är F = q×E = 50000×1,602×10-19 = 8,01×10-15N
Nu är det faktiskt så att vi kan räkna på elektronens rörelse inuti elektronröret som en kaströrelse(om vi bortser från gravitationen). I vår kaströrelse är alltså kraften som pressar elektronen mot den positiva plattan 8,01×10-15N.
Kom ihåg att sträckan i x-led kunde beräknas med formeln:
I vårt fall är då s = 20Mm/s×t
Nu måste vi dock räkna ut t. För att göra detta tar vi fram en annan gammal formel:
Eftersom elektronen går in i elektronstråleröret helt vågrätt så har vi ingen v0y, och y0 = 0,012m.
Eftersom F = m×a så är:
I vårt fall är alltså
När elektronen når den positiva plattan är y = 0.
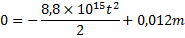
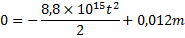
Om vi löser ut t ur denna formel så får vi:
Nu sätter vi in detta i
s = 20Mm/s×t så får vi:
s = 20Mm/s×1,65×10-9 s = 0,033
Svar: sträckan s är 0,033m
Kondensator
En kondensator är en komponent som har förmågan att lagra laddning. Den består av två plattor och något material mellan dessa, exempelvis plast. När den kopplas in till en strömförande krets har den förmågan att lagra viss elektrisk ström. När strömmen lagras kommer en ökande spänning att lägga sig över kondensatorn. Kondensatorn kan laddas upp tills lika stor spänning som det ligger över strömkällan och det är alltså spänningen över kretsen som avgör hur mycket man kan ladda upp en kondensator.
Att räkna på kondensatorer
Nu ska vi införa ett nytt begrepp som man brukar använda när man pratar om kondensatorer, nämligen kapacitans(C), vilken mäts i farad.
Så här kan man räkna på laddningen som en kondensator kan ackumulera:
Q = C×U
Exempel på kondensator, plattkondensator
Kapacitansen för kondensatorn beror främst på materialaspekter. Hur den ser ut, vilket ämne som ligger emellan dess skivor med mera. Plattkondensatorn är dock ett vanligt exempel på kondensatorer som ofta förekommer på prov.
Såhär räknar man på kapacitansen hos en plattkondensator:
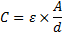
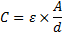
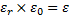
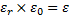
A = area på plattorna
d = avståndet mellan plattorna
εr är vad man kallar den relativa kapacitiviteten.
ε0 = 8,9×10-12 F/m vilket är kapacitiviteten i vakuum.
Energin som kan ackumuleras i en kondensator
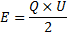
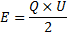
Detta är alltså energin hos en fulladdad kondensator.
Koppling av kondensatorer
Nu ska vi titta på hur hur stor den totala kapacitansen blir när vi kopplar ihop flera kondensatorer. Vi kan seriekoppla och parallellkoppla kapacitanserna.
Parallellkoppling
Seriekoppling
Observera att detta är precis tvärtemot hur det fungerar när man räknar på den totala resistansen hos kopplade resistorer.