Induktion

Induktion har många olika betydelser. Här tar vi upp vad induktion innebär för fysikerna.

Introduktion – Induktion

Detta är ett väldigt intressant fenomen som är helt avgörande för att vår vardag ska fungera som den gör. Induktion går i stora drag ut på att vi har en ledare som det inte går ström genom. Denna ledare ligger i ett magnetfält. Vi låter sedan ledaren röra på sig med en allt större hastighet i magnetfältet och upptäcker då att det går en ström genom ledaren så länge ledarens hastighet i magnetfältet förändras. Vi säger att det induceras en ström.

Induktion kan alltså som ovan uppkomma i en ledare men det kan även inträffa i en spole. Enda kriteriet för att induktion ska uppkomma är att antingen magnetfältet som påverkar ledaren/spolen ändras eller att ledarens/spolens rörelse i magnetfältet förändras.

Observera att induktion enbart uppkommer under den tid då magnetfält eller rörelse förändras. Vi har alltså ingen induktion vid konstant hastighet eller vid ett konstant magnetfält.

Från förra kapitlet kommer vi ihåg att en ledare som det går ström genom och ligger i ett magnetfält påverkas av en kraft. Alltså bör induktionen ge upphov till en kraft.

Lenz formulerade hur denna kraft är riktad i en välkänd lag som heter Lenz lag. Innan du läser denna är det viktigt att du förstår att vid induktion kan man säga att det induceras en ström, ett magnetfält eller en spänning. Det induceras egentligen alla tre eftersom de är beroende av varandra.

---

Lenz lag

Den inducerade spänningen/strömmen/magnetfältet har en sådan riktning att den motverkar orsaken till sin egen uppkomst.

I lättare ord betyder detta att om en ledare accelererar neråt i ett magnetfält så kommer det att induceras ett sådant magnetfält och en sådan ström som ger en kraft på ledaren uppåt. Induktionen motverkar helt enkelt förändringen. Den inducerade kraften kommer dock bara bromsa upp rörelsen lite.

Ett annat fall som är intressant är motsatsen, en ledare faller i en retarderande (motsats till accelererande) rörelse. Då kommer ett magnetfält och en ström induceras så att vi får en kraft som är riktad neråt och skjuter på ledaren som faller.

---

Inducerad spänning över rak ledare som rör sig i ett magnetfält

Nu ska vi försöka härleda en formel till hur stor den inducerade spänningen blir på en rak ledare som rör sig i ett magnetfält.

När ledaren rör sig påverkas den ju uppenbart av en kraft från magnetfältet. Varje laddad partikel påverkas också av en kraft från magnetfältet (se kap 8 ) och det är här vi börjar vår härledning:

I detta fall accelererar ledaren. Alltså uppkommer induktion. När ström induceras kommer det att bildas en plussida och en minussida på ledaren. Ett elektriskt fält bildas då över ledaren och även en kraft uppstår:

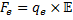
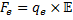
Detta är alltså dem kraft som induktionen åstadkommer. Den är enligt Lenz lag riktad åt motsatt håll gentemot kraften som magnetfältet ger upphov till.

Nu tänker vi oss att F_e ökar tills den är lika stor som F_m. Då kommer krafterna att ta ut varandra och induktionen kommer att upphöra då föremålet inte accelererar längre utan håller en konstant hastighet:

F_e = F_m

Alltså:

Alltså:

I kapitel sju såg vi att 

I detta fall är U den inducerade spänningen e och d är ledarens längd l.

Alltså:

Vi har nu kommit fram till att den inducerade spänningen 

Kom ihåg att det viktigaste kanske inte är att ni förstår hela härledningen fullt ut utan att ni kan formeln!

Magnetiskt flöde

Magnetiskt flöde är en ny spännande enhet som definieras på följande sätt:

(enheten är 1 Weber)

Alltså är det magnetiska flödet lika med den magnetiska flödestätheten multiplicerat med den area som flödestätheten träffar.

Observera att B i detta fall är den flödestäthet som träffar arean vinkelrätt. Kommer flödestätheten in snett är alltså B den vertikala komposanten.

Den inducerade spänningen över en slinga/spole i ett föränderligt magnetfält

Detta tänker vi inte försöka härleda då det blir lite för krångligt och onödigt. Här kommer formeln rakt av, håll till godo!

I denna formel är N antal varv spolen har. Är det en slinga är N alltså lika med 1.

innebär det magnetiska flödets förändring med tiden.

Självinduktion

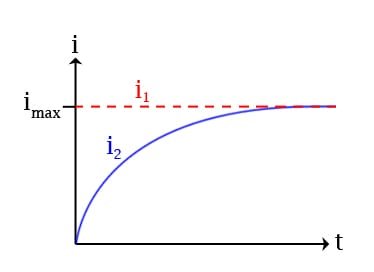
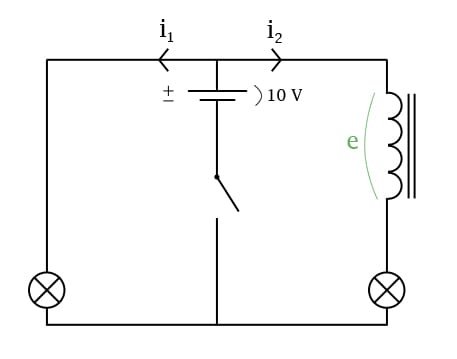
Självinduktion är ett fenomen som kan iakttas när vi har en krets med en spole. För att tydligt visa självinduktion har vi i bilden nedan satt in en spole i en krets där strömmen går i två ritningar. På bägge sidor finns en lampa, lamporna är identiska. På ena sidan finns dock en spole med en järnkärna i. När vi slår på strömbrytaren ser vi att den lampan som finns på sidan utan spole tänds direkt medan den andra lampan tar några ögonblick innan den tänds. Den tänds dessutom lite successivt.

Detta händer:

• Detta är ett typiskt exempel på självinduktion. När strömbrytaren slås på kommer en ström(i2) att gå genom spolen. Det uppkommer då ett magnetfält i och en spänning över spolen.
• Denna spänningsförändring kommer då att motverkas av en motsatt riktad inducerad spänning enligt Lenz lag.
• Vi har då en spänning U över batteriet men denna motverkas av en inducerad spänning e över spolen. Nettospänningen på denna sida av kretsen blir då Unetto= U-e. Vi får då en lägre ström som når lampan. När induktionen sedan minskar och blir 0 är Unetto=U och då lyser lampan lika starkt som den andra.

Hur stor är e vid självinduktion?

Vi måste nu introducera begreppet induktans(L) som vi inte tänker definiera närmare vad det är. Ytterst ytligt kan man säga att induktansen är produkten av olika spolegenskaper, bland annat spolens varvantal och bottenarea.

Vi tänker inte härleda denna formel heller, men här kommer den:

Den inducerade spänningen vid självinduktion är alltså lika med spolens induktans multiplicerat med strömändringen per tidsenhet genom spolen.

---

Växelström

Experiment

Växelström är ett fenomen som vi har mycket stor användning av idag. Bland annat används detta i våra generatorer och fenomenet bygger på induktion.

Växelström uppkommer när vi låter en slinga rotera i ett magnetfält. Olika stor andel av flödestätheten kommer då att träffa slingan vinkelrätt.

Först ligger slingan vinkelrätt mot magnetfältet. Då träffar magnetfältet 100 % av slingans area. Detta illustreras ovan.

Vi låter slingan rotera (v) grader. Då kommer bara en del av slingan som fortfarande ligger vinkelrätt mot magnetfältet att påverkas. I figuren ovan är detta basen A₁.

Med enkel trigonometri blir denna bas

Sedan låter vi slingan rotera ännu mer så att den står parallellt med magnetfältet. Då kommer ingen del av slingan att träffas av magnetfältet.

Vi låter slingan rotera (v) grader till. Då kommer bara en del av slingan som fortfarande ligger vinkelrätt mot magnetfältet att påverkas. I figuren ovan är detta basen A₁.

Med enkel trigonometri blir denna bas

Observera att denna area blir lika stor som när vi enbart hade roterat (v) grader men det är andra sidan av slingan som är riktad uppåt.

Analys

I detta experiment kan vi se att magnetfältet träffar olika stora delar av arean vid olika tidpunkter. Alltså är det magnetiska flödet olika vid olika tidpunkter.

Det börjar i sitt maximum då hela sidan träffas men kommer sedan att sjunka mer och mer tills slingan går parallellt med magnetfältet och flödet är noll.

Sedan ökar flödet igen men med flödestätheten träffar den andra sidan av slingan. Alltså blir flödet negativt till ett maxbelopp då slingan vridit sig 1800 från ursprungspunkten.

När slingan vridits 2700 från ursprungsläget är flödet nere i noll igen då slingan ligger parallellt med magnetfältet och sedan ökar det för att nå upp i sitt positiva toppvärde när slingan vridits ett helt varv.

Resultat

Från vårt utmärkta experiment kan vi konstatera att det magnetiska flödet ändras periodiskt.

Då är

och

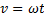
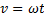
(se periodisk rörelse)

Flödet är beroende av slingans vinkel jämfört med magnetfältet på följande vis:

Om vi då ersätter v med ωt så får vi:

Genom att derivera får vi flödesförändringen per tidsenhet:

Ok, då vet vi det, nu ska vi titta på formeln för inducerad spänning i slinga:

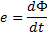
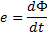
Vi ersätter  med  och inser då raskt att den inducerade spänningen i en slinga med växelström fås av formeln:

Om vi istället har en spole som roterar lägger man bara till spolens varvantal(N):

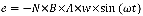
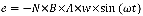
Du inser säkert att har ett toppvärde och dessa kan då ersättas med Û (eller ê som i formeln).

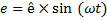
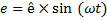
Växelspänningen beror alltså sinusformat av tiden!

Fler viktiga lagar om växelström

Här kommer en kort uppställning av de viktigaste lagarna inom växelström. Dessa gäller enbart när en resistor är kopplad till växelströmskretsen:

Observera att ovanstående är samma lag som den vi kom fram till i exemplet ovan, har bytt ut beteckningen e mot u.

Effektivvärdet

Som ni förstår så varierar spänningen och strömmen med tiden så hur ska vi mäta detta?

Vi använder då effektivvärdet för växelspänningen(-strömmen) och denna definieras på följande vis:

Växelspänningen ger upphov till en genomsnittlig effektutveckling. Om växelspänningen är så stor att den i genomsnitt skulle ge samma effektutveckling som i en likspänningskrets med en resistor så är detta spänningens effektivvärde.

Precis samma resonemang gäller med strömmens effektivvärde.

Här följer formler för hur vi räknar på effektivvärden för ström och spänning :

Effektivvärdet för ström(I)

Effektivvärdet för spänning(U)

Växelström i kretsar med annat än resistorer

Nu är det ju så att vi inte alltid kopplar resistorer till växelströmskretsarna. Ibland kan det exempelvis vara en kondensator eller en spole. Effektivvärdena kommer då inte att bli annorlunda men toppspänningen och toppströmmen behöver inte längre ligga i fas. I kretsen med resistorn följde strömmen och spänningen varandra fint och hade sina toppar och dalar på samma ställen.

En spole eller en kondensator kan fördröja spänningen och göra att den halkar efter strömmen, därför behöver vi modifiera formeln för spänning i en viss tidpunkt för att den ska gälla för alla växelströmskretsar:

Som ni märker är formeln för strömmen i en viss tidpunkt oförändrad men spänningskurvan kommer att skjutas bakåt med (a) grader, vilket är fasförskjutningen.

Fasförskjutningen i:

1. En resistor är 0 grader(sin(ωt+a) blir då sin(ωt))
2. En spole har fasförskjutningen 90 grader
3. En kondensator har fasförskjutningen 270 grader.

Effektutvecklingen

Vi har redan varit inne och nosat på effektutvecklingen. I en likströmskrets vet vi att effektutvecklingen(P) är så här stor:

I en växelströmskrets är den genomsnittliga effektutvecklingen så här stor:

(U och I är effektivvärden)

Detta betyder att en spole som har fasförskjutningen 90 grader och en kondensator som har fasförskjutningen 270 grader inte har någon effektutveckling!

---

Transformator

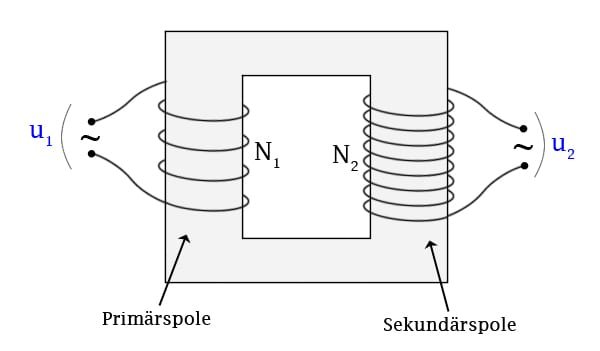
Transformatorer används för att reglera spänningen.

Vi har en primärspole och en sekundärspole. Dessa spolar består av en sluten järnkärna och två ledare lindade runt som på bilden. Genom att låta en spänning U₁ läggas över primärspolen kommer vi att orsaka en magnetfältsändring. Denna magnetfältsändring kommer kännas av i sekundärspolen och spänningen U₂ kommer att induceras i sekundärspolen.

På följande vis beror spänningen U2 av antalet varv som primär och sekundärspole är lindade med:

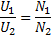
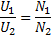
Alltså kommer spänningen man får ut i sekundärspolen i allra högsta grad att påverkas av hur de bägge spolarna lindas.

Vi kan dock inte få en högre spänning och en större ström samtidigt. Då hade ju energin ökat och vi hade byggt oss en fin evighetsmaskin. Haken är alltså att om vi transformerar upp spänningen så blir strömstyrkan lägre.

Mer konkret: effektutvecklingen är lika stor i primär- och sekundärspolen.

Alltså:

Om vi transformerar ner spänningen får vi upp strömmen och tvärtom.

Detta används i högspänningsledningar. Genom att ha hög spänning och låg ström minskar vi energiförlusterna till ett minimum.