Vågor är mer än de man ser vid stranden. Många fenomen i vår omgivning, till exempel vår hörsel, beror på svängande rörelser! Här följer en sammanfattning av kapitlet vågor i kursen Fysik 2.
Inledande våg-begrepp
Vi börjar med några inledande begrepp för att förstå kapitlet.
Våg
Är en svängning som utbreder sig i rummet. Viktigt att komma ihåg att ingen materia förflyttas, enbart energi.
Mekanisk våg
Utbreder sig i ett medium, alltså i gas, vätska eller fast ämne.
Transversell våg
Svängningen sker vinkelrätt mot vågens utbredningsriktning.
Longitudinell våg
Svängningen sker parallellt med vågens utbredningsriktning.
En transversell våg brukar ritas upp på följande vis och beskrivas med termer som figuren nedan visar:


Detta diagram visar hur vågen ser ut och hur den utbreder sig.
A = amplituden är högsta eller lägsta nivån från jämviktsläget.
λ (lambda)= våglängden, alltså hur lång vågen är i horisontalplan.
Ovanstående diagram beskriver alltså vågens rörelse vertikalt jämfört med horisontalt.
Ofta är det även intressant att titta på rörelsen i en viss punkt beroende av tiden. Alltså hur denna punkt förflyttas vertikalt när vågen går igenom den. Diagrammet nedan beskriver visar en sådan undersökning:


T = Den tid det tar för en punkt att från att den befunnit sig i jämviktsläget genomföra hela svängningen, upp-ner- och tillbaka till jämviktsläget.
Vågutbredningshastigheten
Nu ska vi titta på hur perioden(T) och våglängden(lambda) hänger samman.
Vågutbredningshastigheten(v)=våglängden(lambda)/perioden(T) eller


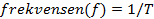
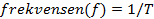
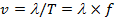
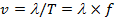
Vågor som reflekteras
En våg som reflekteras mot ett tunnare medium reflekteras rättvänt tillbaka.
En våg som reflekteras mot ett tätare medium reflekteras spegelvänt tillbaka. Bilderna nedan illustrerar en förloppet när en våg reflekteras mot ett tätare medium.
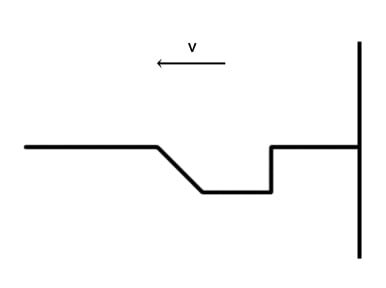
Vid första bilden är vågen på väg mot det tätare medium.


Vid andra bilden (nedan) har vågen reflekterats och är på väg tillbaka, med samma form och fart, fast spegelvänd.

Superpositionsprincipen
Nu ska vi se vad som händer när två vågor möter varandra. När de möts adderas deras amplituder i varje punkt de korsar varandra. Detta illustreras i bilderna nedan.
I bilden rör sig de två vågorna mot varandra och ska snart mötas.


I bilden nedan har de precis nått fram till varandra och börjat korsningen. Fyrkantens högra och “prispallens“ vänstra del ligger i samma punkt och amplituderna för de bägge delarna adderas.
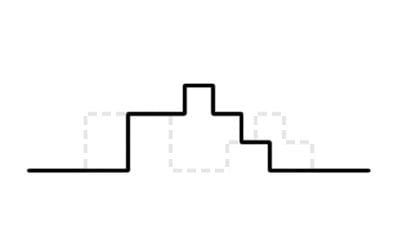

När de ligger precis på varandra så adderas amplituderna och bildar en gemensam svängning som ser ut såhär.


Efter korsningen tar de båda vågorna sin ursprungliga form.
Detta är ett exempel på positiv interferens.
Vid negativ interferens försvagar vågorna varandra när de möts. Detta sker om deras amplituder är riktade åt olika håll.
Stående vågor
Detta är ett fenomen som inträffar när vågor möter varandra eller interfererar på ett speciellt sätt. Tänk dig en vågmaskin som konstant pumpar vågor med samma frekvens mot ett tunnare medium. Vågorna reflekteras rättvänt och möter de svängningar som vågmaskinen har startat lite senare. Vi prövar sedan att variera frekvensen hos vågmaskinen och upptäcker att vid vissa frekvenser bildar tråden ett mönster av bukar (ovaler). Vi ser också att desto högre frekvensen blir, desto fler bukar bildas. Detta sker vid sådana frekvenser att de inkommande vågorna ligger precis på de reflekterade.
Vi förtydligar med några bilder:
Två likadana vågor med samma amplitud och våglängd infaller mot ett tunnare medium.


När den ena vågen reflekterats möts de två vågorna och de förstärker varandra. Detta sker i bilden nedan.


Nu skickar vi istället många vågor mot det tunnare medium:


Så här ser det då ut när de möter varandra och interfererar:


Detta sker för att den infallande och den reflekterande vågfronten ligger på varandra och förstärker varandra i varje punkt.
Grundton och övertoner
Vi hävdade inledningsvis att fler bukar bildas desto högre frekvensen är. Om vi utför experimentet och ökar frekvensen successivt märker vi att en stående våg uppkommer varje gång ett helt antal bukar får plats på tråden mellan vågkällan och det tunna medium.
När bara en buk får plats, kallar man det att tråden svänger i sin grundton:


Ändarna kallas nodpunkter då de alltid är stilla.
Avståndet mellan två noder är alltid en halv våglängd.
I detta fall är alltså L(trådens längd) = en halv våglängd(λ/2).
I bilden nedan får två bukar plats. Tråden svänger i sin första överton:
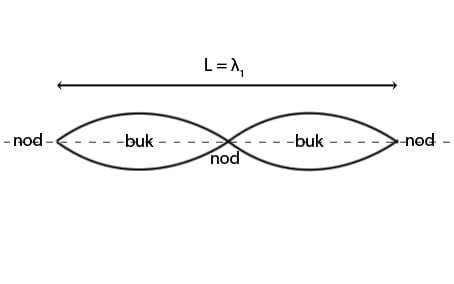

Här har vi tre nodpunkter och två bukar, L = λ1
I bilden nedan har vi fyra noder och tre bukar, L = 3λ2/2. Får tre bukar plats som i bilden nedan svänger tråden i andra övertonen.
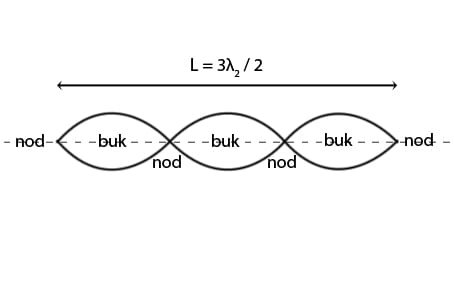

De stående vågorna fortsätter uppkomma enligt detta mönster i all evighet enligt teorin.
Stående vågor i pipor
Om du blåser i en pipa uppstår det faktiskt stående vågor.
Det finns två sorters pipor:
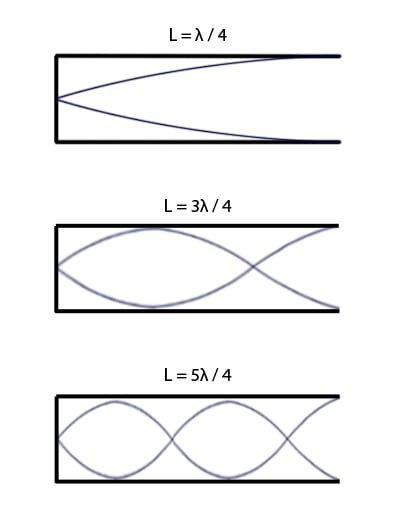
Den öppna pipan, som bilden nedan visar, har grundtonen λ/2, 1:a övertonen λ osv.


Den slutna pipan som bilden under visar har grundtonen λ/4, 1:a övertonen 3λ/4 osv.

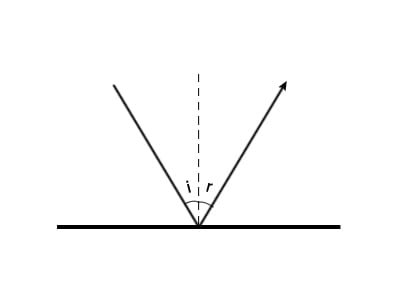
Reflektion av vågor
Reflektionen sker precis som med ljus vilket innebär att exempelvis vattenvågor som kommer in mot en vägg med 45 graders vinkel går ut med 45 graders vinkel mot normalen. Infallsvinkeln = reflektionsvinkeln, precis som vi lärde oss redan i Fysik A.

Refraktion/Brytning
Om exempelvis vattenvågor går från djupare till grundare vatten, dvs från tätare till tunnare vattenskikt bryts vågorna mot normalen.


Viktigt att veta när det gäller vågor som går från ett ämne till ett annat är att frekvensen förblir densamma. Vågutbredningshastigheten och våglängden förändras dock.
Tre bra formler:
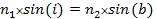
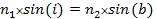
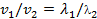
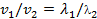


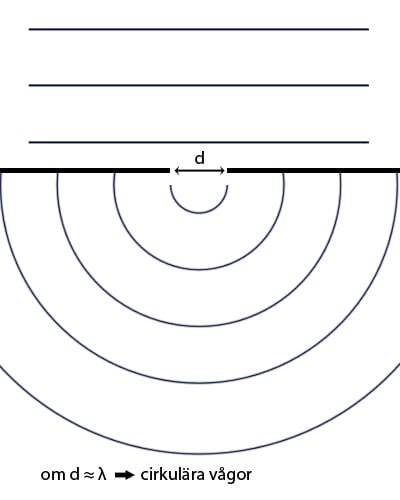
Diffraktion/Böjning
Reflektion och refraktion var som sagt gammal skåpmat, men här kommer något nytt igen. När vågor infaller mot en springa vars bredd är ungefär lika stor som vågens våglängd så bildas cirkulära vågor på andra sidan springan.

Interferens mellan två punktkällor
Ljud är ju som känt också vågor, så kan ljudvågor också förstärka och ta ut varandra? Ja, det kan de faktiskt. Detta illustrerar vi med bilden nedan där två ljudkällor i fas sänder ut vågor i cirklar med samma frekvens och amplitud.


För att enklare förklara tänker vi oss ljudvågor som en transversell vågrörelse. Varje cirkel motsvarar ljudvågens högsta punkt och mitt mellan cirklarna (i dalarna) har vi ljudvågens lägsta punkt. Där två cirklar korsar varandra får vi ljudförstärkning eftersom de två ljudvågorna interfererar i sina högsta lägen. Vi får även ljudförstärkning där två dalar korsar varandra. Linjerna som är inritade motsvarar alla punkter där ljudmaxima infinner sig.
När däremot en cirkel träffar en dal är ena ljudvågen i sitt högsta läge och den andra i sitt lägsta. Då tar vågorna ut varandra och vi får punkter med ljudminima. De streckade linjerna visar punkter med ljudminima.
Nu undrar ni förstås hur man räknar på detta?
Tidigare såg vi att två ljudvågor i fas förstärker varandra och två ljudvågor ur fas försvagar varandra. Eftersom vågorna skjuts ut samtidigt från ljudkällorna och i fas så måste vi ha en vägskillnad för att få dem ur fas. Vågorna ligger ur fas om den ena vågen ligger en halv våglängd efter (eller 1,5λ eller 2,5λ osv.). Detta händer när den ena vågen har gått en halv våglängd längre sträcka.
Alltså:
Om skillnaden i sträcka AB-AC är ett udda antal halva våglängder så får vi ett ljudminima
Om skillnaden i sträcka AB-AC är ett antal hela våglängder så får ett ljudmaxima
Ljus som vågor
I nästa kapitel får ni läsa om vågor i en annan form – nämligen som ljus!
Vågor – Fysik 2 – videomaterial
Här har Jimmy Gustafsson gjort videor med sammanfattningar av kapitlet vågor.

