Ljus är ett intressant fenomen som kan beskrivas på många sätt. Vi har tidigare betraktat ljus som strålar eller som vågor men nu ska vi titta på ljus från ett nytt perspektiv, nämligen som partiklar. Dessutom ska vi titta lite på hur föremål utstrålar och absorberar energi samt hur man kan räkna på detta.
Emittans
Det första begreppet vi ska prata om är emittans. Emittansen beskriver egentligen hur stor effekt ett föremål strålar ut per ytenhet.
Emittansen brukar betcknas M och har enheten W/m2.
Så här räknar man på emittansen:
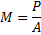
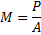
Viktigt att notera är att alla föremål har en emittans. Dock så varierar den mycket mellan olika material.
Allmänt kan man säga att den ökar med temperatur. Dessutom har mörka, matta ytor ofta hög emittans.
Absorbtion av ljus
Absorption är ett föremåls benägenhet att absorbera energi från omgivningen.
Absolut svartkropp
I teorin brukar man ibland tala om föremål som absorberar all infallande strålning. Detta brukar kallas en absolut svartkropp. Många föremål beter sig nästan som absoluta svartkroppar och det kan vara givande att utgå ifrån detta i vissa beräkningar. Solen beter sig exempelvis i princip som en absolut svartkropp.
Wiens förskjutningslag
Nu är det så att emittansen för ett föremål är olika vid olika våglängder. Föremålet emitterar energi av olika våglängder och självklart är det någon våglängd där emittansen är högst. Denna våglängd brukar betecknas som λm.


Våglängden för den maximala emittansen beror av temperaturen på följande vis (wiens förskjutningslag):


Viktigt att påpekar är att temperaturen mäts i Kelvin!
Stefan-Boltzmanns lag
Emittansen är också beroende av temperaturen. Stefan Bolzmann beskrev detta med denna formel:
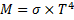
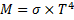
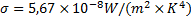
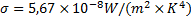
Observera att temperaturen ska mätas i Kelvin även här!
Fotoelektrisk effekt
I början av 1900-talet levde fysikern Max Planck. Han lade grunden till en helt ny bild av hur ljus beter sig. Han påbörjade arbetet, som Einstein avslutade, på en teori där energi inte strålar kontinuerligt utan i en sorts ”energipaket”, så kallade fotoner. Detta är en teori man kan använda för att förklara den fotoelektriska effekten. Denna går ut på att man kan få elektroner att slitas från en metallplatta genom att bestråla den med strålning av tillräckligt hög frekvens.
Nedan beskrivs närmare den fotoelektriska effekten
Vi tänker oss att vi har en metallplatta. Om vi tillför denna platta tillräckligt mycket energi så kommer elektroner att kunna frigöra sig från plattan. Vi tillför plattan energi genom att bestråla den med ljus. Först bestrålar vi plattan med rött ljus och ser att ingenting händer. Vi ökar intensiteten på det röda ljuset men ingenting händer fortfarande. Vi prövar att låta blått ljus infalla mot metallplattan och observerar då att elektroner börjar frigöras från den. Nu provar vi att öka intensiteten på det blåa ljuset och ser då att fler elektroner sliter sig loss.
Ovanstående hade varit helt orimligt om vi beskriver ljuset som vågor, alltså kontinuerlig energi. Då skulle nämligen en högre intensitet rött ljus ge en större energi till plattans elektroner vilket det uppenbart inte gör. Vi tänker oss istället ljuset som små energiportioner(fotoner). Vi tänker oss att varje foton i det röda ljuset har en viss bestämd energi och varje foton i det blåa ljuset har en viss energi. Det krävs en viss energi för att lösgöra en elektron ur plattan och eftersom det röda ljuset inte uppnår denna energi när intensiteten ökar kan man konstatera att fotoner inte kan slås ihop. Fotonernas energi måste alltså överstiga den energi som krävs för att frigöra en elektron ur plattan. Det blå ljuset har energirikare fotoner än det röda, och varje foton har tillräckligt mycket energi för att frigöra en elektron ur plattan. Om vi ökar intensiteten hos det blå ljuset kommer fler fotoner att träffa plattan och därmed kommer fler elektroner frigöras.
Det är ovanstående fenomen som kallas fotoelektrisk effekt, och det finns en hel del att räkna på när det gäller detta fenomen:
Fotonens energi:
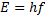
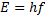
h är i detta fall Plancks konstant som ligger på 6,63×10-34 Js, och f är ljusets frekvens.
Om energin det krävs för att en elektron ska frigöras från plattan betecknas Eu så kommer en elektron att frigöras om
hf > Eu.
Eu är specifik för metallen.
Einsteins fotoelektriska ekvation
Einstein funderade på huruvida fotonen behövde innehålla exakt samma mängd energi som Eu för att elektronen skulle brytas ut men insåg att restenergin omvandlades till rörelseenergi hos elektronen.
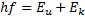
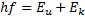
Viktig summering:
Högre intensitet på ljuset ger fler men inte energirikare fotoner.
Comptonspridning
Nu har vi alltså beskrivit ljus som fotoner, med en viss energimängd. Enligt denna modell beter sig ljuset som partiklar. Nu tänker vi oss att fotoner får infalla och krocka med en elektron i vila. Detta gör att fotonen ändrar riktning, men även att elektronen far iväg åt ett annat håll. Fotonen beter sig alltså som en partikel även i detta fall, och ”puttar” elektronen när kollisionen sker.
Enligt energiprincipen måste fotonen förlora energi om elektronen får energi, och mer specifikt så bör förhållandet se ut såhär (elastisk stöt):
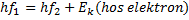
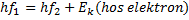
Utifrån detta resonemang, och en rad beräkningar som vi inte går in som vi inte går in på här kan man komma fram till att fotonens rörelsemängd kan beskrivas på följande vis:
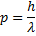
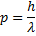
Partiklars vågegenskaper
Nu har vi alltså insett att fotoner kan beskrivas precis som partiklar, alltså med en rörelsemängd och en energi. Men nu funderar vi över det motsatta; kan partiklar beskrivas som vågor?
Louis de Broglie kom fram till att detta gick alldeles utmärkt och han visade hur stor våglängden för partikeln blev med följande enkla beräkningar:
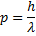
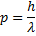


Om vi slår ihop ovanstående formler(fotonens respektive partikelns rörelsemängd) så får vi:


Detta kallas De Broglies fromel.
Viktigt att notera är att partiklars vågegenskaper endast blir märkbara om våglängden är ungefär lika stor som partikelns storlek.
Summering
Nu har vi sett att ljus ibland beter sig som partiklar. Dock hade vi ju även vår gamla modell där ljus var en vågrörelse, så vilket är sant? Idag använder vi faktiskt båda modellerna, då de kan förklara olika fenomen hos ljuset. Vi förlikar oss helt enkelt med att ljus både kan bete sig som en vågrörelse och som partiklar.

